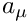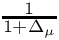Namespaces
namespace	detail

namespace	thdm

Classes
class	Config_options
	configuration for the calculation of $a_\mu$ More...

class	EInvalidInput

class	EPhysicalProblem

class	EReadError

class	Error

class	ESetupError
	Spectrum generator was not setup correctly. More...

struct	Flip_sign

class	GM2_slha_io
	class for reading input files and writing SLHA output files More...

class	MSSMNoFV_onshell
	contains the MSSMNoFV parameters in the on-shell scheme More...

class	MSSMNoFV_onshell_mass_eigenstates
	model class with routines determine masses, mixings and EWSB More...

class	MSSMNoFV_onshell_physical
	MSSMNoFV pole masses and corresponding mixings. More...

class	MSSMNoFV_onshell_problems
	contains problem and warning flags More...

class	MSSMNoFV_onshell_soft_parameters
	contains soft-breaking parameters of the MSSMNoFV model More...

class	MSSMNoFV_onshell_susy_parameters
	contains SUSY parameters of the MSSMNoFV model More...

class	RAII_save
	Saves value of variable and restores it at destruction. More...

class	SM

class	THDM
	Contains routines to determine the THDM parameters. More...

class	THDM_mass_eigenstates
	model class with routines for determing masses and mixinga and EWSB More...

class	THDM_parameters
	Contains the parameters of the THDM model. More...

class	THDM_problems
	contains problem and warning flags More...

Functions
double	dilog (double x) noexcept
	Real dilogarithm $\operatorname{Li}_2(x)$ .

std::complex< double >	dilog (const std::complex< double > &z) noexcept
	Complex dilogarithm $\mathrm{Li}_2(z)$ .

double	clausen_2 (double x) noexcept
	Clausen function $\mathrm{Cl}_2(\theta) = \mathrm{Im}(\mathrm{Li}_2(e^{i\theta}))$ .

template<typename Derived >
unsigned	closest_index (double mass, const Eigen::ArrayBase< Derived > &v)

template<class Derived >
bool	is_equal (const Eigen::ArrayBase< Derived > &a, const Eigen::ArrayBase< Derived > &b, double precision_goal)

template<class Derived >
bool	is_zero (const Eigen::ArrayBase< Derived > &a, double eps)

template<int M, int N>
void	normalize_to_interval (Eigen::Matrix< double, M, N > &m, double min=-1., double max=1.)
	Normalize each element of the given real matrix to be within the interval [min, max].

template<typename DerivedArray , typename DerivedMatrix >
void	move_goldstone_to (int idx, double mass, Eigen::ArrayBase< DerivedArray > &v, Eigen::MatrixBase< DerivedMatrix > &z)
	The element of v, which is closest to mass, is moved to the position idx.

template<class Real , int Nsrc, int Ncmp>
Eigen::Array< Real, Nsrc - Ncmp, 1 >	remove_if_equal (const Eigen::Array< Real, Nsrc, 1 > &src, const Eigen::Array< Real, Ncmp, 1 > &cmp)
	Returns all elements from src, which are not close to the elements in cmp.

template<class Real , int N>
void	reorder_vector (Eigen::Array< Real, N, 1 > &v, const Eigen::Array< Real, N, 1 > &v2)
	reorders vector v according to ordering in vector v2

template<class Derived >
void	reorder_vector (Eigen::Array< double, Eigen::MatrixBase< Derived >::RowsAtCompileTime, 1 > &v, const Eigen::MatrixBase< Derived > &matrix)
	reorders vector v according to ordering of diagonal elements in mass_matrix

template<typename Derived >
void	symmetrize (Eigen::MatrixBase< Derived > &m)

double	F1C (double) noexcept
	, Eq (54) arXiv:hep-ph/0609168

double	F2C (double) noexcept
	, Eq (55) arXiv:hep-ph/0609168

double	F3C (double) noexcept
	, Eq (37) arXiv:1003.5820

double	F4C (double) noexcept
	, Eq (38) arXiv:1003.5820

double	F1N (double) noexcept
	, Eq (52) arXiv:hep-ph/0609168

double	F2N (double) noexcept
	, Eq (53) arXiv:hep-ph/0609168

double	F3N (double) noexcept
	, Eq (39) arXiv:1003.5820

double	F4N (double) noexcept
	, Eq (40) arXiv:1003.5820

double	Fb (double, double) noexcept
	, Eq (6.3b) arXiv:1311.1775

double	Fa (double, double) noexcept
	, Eq (6.3a) arXiv:1311.1775

double	G3 (double) noexcept
	, Eq (6.4a) arXiv:1311.1775

double	G4 (double) noexcept
	, Eq (6.4b) arXiv:1311.1775

double	Iabc (double, double, double) noexcept
	$I_{abc}(a,b,c)$ (arguments are interpreted as unsquared)

double	f_PS (double z) noexcept
	Calculates $f_{PS}(z)$ , Eq (70) arXiv:hep-ph/0609168.

double	f_S (double z) noexcept
	Calculates , Eq (71) arXiv:hep-ph/0609168.

double	f_sferm (double z) noexcept
	Calculates $f_{\tilde{f}}(z)$ , Eq (72) arXiv:hep-ph/0609168.

double	f_CSl (double z) noexcept
	Calculates Barr-Zee 2-loop function for diagram with lepton loop and charged Higgs and W boson mediators, Eq (60), arxiv:1607.06292, with extra global prefactor z.

double	f_CSd (double xu, double xd, double qu, double qd) noexcept
	Eq (61), arxiv:1607.06292, with extra global prefactor xd.

double	f_CSu (double xu, double xd, double qu, double qd) noexcept
	Eq (62), arxiv:1607.06292, with extra global prefactor xu.

double	F1 (double w) noexcept
	$\mathcal{F}_1(\omega)$ , Eq (25) arxiv:1502.04199

double	F1t (double w) noexcept
	$\tilde{\mathcal{F}}_1(\omega)$ , Eq (26) arxiv:1502.04199

double	F2 (double w) noexcept
	$\mathcal{F}_2(\omega)$ , Eq (27) arxiv:1502.04199

double	F3 (double w) noexcept
	$\mathcal{F}_3(\omega)$ , Eq (28) arxiv:1502.04199

double	FPZ (double x, double y) noexcept
	Barr-Zee 2-loop function with fermion loop and pseudoscalar and Z boson mediators.

double	FSZ (double x, double y) noexcept
	Barr-Zee 2-loop function with fermion loop and scalar and Z boson mediators.

double	FCWl (double x, double y) noexcept
	Barr-Zee 2-loop function with lepton loop and charge scalar and W boson mediators.

double	FCWu (double xu, double xd, double yu, double yd, double qu, double qd) noexcept
	Barr-Zee 2-loop function with up-type quark loop and charge scalar and W boson mediators.

double	FCWd (double xu, double xd, double yu, double yd, double qu, double qd) noexcept
	Barr-Zee 2-loop function with down-type quark loop and charge scalar and W boson mediators.

double	lambda_2 (double x, double y, double z) noexcept
	Källén lambda function $\lambda^2(x,y,z) = x^2 + y^2 + z^2 - 2xy - 2yz - 2xz$ .

double	Phi (double x, double y, double z) noexcept
	$\Phi(x,y,z)$ function from arxiv:1607.06292 Eq.

template<class Real , class Scalar , int M, int N>
void	svd_eigen (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > u, Eigen::Matrix< Scalar, N, N > vh)

template<class Real , class Scalar , int N>
void	hermitian_eigen (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > *z)

template<int M, int N, class Real >
void	disna (const char &JOB, const Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &D, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &SEP, int &INFO)
	Template version of DDISNA from LAPACK.

template<class Real , class Scalar , int M, int N>
void	svd_internal (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > u, Eigen::Matrix< Scalar, N, N > vh)

template<class Real , class Scalar , int M, int N>
void	svd_errbd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > u=0, Eigen::Matrix< Scalar, N, N > vh=0, Real s_errbd=0, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > u_errbd=0, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *v_errbd=0)

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh)
	Singular value decomposition of M-by-N matrix m such that.

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd)
	Same as svd(m, s, u, vh) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &u_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &v_errbd)
	Same as svd(m, s, u, vh, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s)
	Returns singular values of M-by-N matrix m via s such that `(s >= 0).all()`.

template<class Real , class Scalar , int M, int N>
void	svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Real &s_errbd)
	Same as svd(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int N>
void	diagonalize_hermitian_internal (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > *z)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian_errbd (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > z=0, Real w_errbd=0, Eigen::Array< Real, N, 1 > *z_errbd=0)

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z)
	Diagonalizes N-by-N hermitian matrix m so that.

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd)
	Same as diagonalize_hermitian(m, w, z) except that an approximate error bound for the eigenvalues is returned as well.

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd, Eigen::Array< Real, N, 1 > &z_errbd)
	Same as diagonalize_hermitian(m, w, z, w_errbd) except that approximate error bounds for the eigenvectors are returned as well.

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w)
	Returns eigenvalues of N-by-N hermitian matrix m via w.

template<class Real , class Scalar , int N>
void	diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Real &w_errbd)
	Same as diagonalize_hermitian(m, w) except that an approximate error bound for the eigenvalues is returned as well.

template<class Real , int N>
void	diagonalize_symmetric_errbd (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)
	Diagonalizes N-by-N complex symmetric matrix m so that.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)
	Same as diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)
	Same as diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s)
	Returns singular values of N-by-N complex symmetric matrix m via s such that `(s >= 0).all()`.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)
	Same as diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , int N>
void	diagonalize_symmetric_errbd (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)
	Diagonalizes N-by-N real symmetric matrix m so that.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)
	Same as diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)
	Same as diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s)
	Returns singular values of N-by-N real symmetric matrix m via s such that `(s >= 0).all()`.

template<class Real , int N>
void	diagonalize_symmetric (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)
	Same as diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int M, int N>
void	reorder_svd_errbd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > u=0, Eigen::Matrix< Scalar, N, N > vh=0, Real s_errbd=0, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > u_errbd=0, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *v_errbd=0)

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh)
	Singular value decomposition of M-by-N matrix m such that.

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd)
	Same as reorder_svd(m, s, u, vh) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &vh, Real &s_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &u_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &v_errbd)
	Same as reorder_svd(m, s, u, vh, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s)
	Returns singular values of M-by-N matrix m via s such that `(s >= 0).all()`.

template<class Real , class Scalar , int M, int N>
void	reorder_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Real &s_errbd)
	Same as reorder_svd(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , int N>
void	reorder_diagonalize_symmetric_errbd (const Eigen::Matrix< std::complex< Real >, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , int N>
void	reorder_diagonalize_symmetric_errbd (const Eigen::Matrix< Real, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)
	Diagonalizes N-by-N symmetric matrix m so that.

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)
	Same as reorder_diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)
	Same as reorder_diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s)
	Returns singular values of N-by-N symmetric matrix m via s such that `(s >= 0).all()`.

template<class Real , class Scalar , int N>
void	reorder_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)
	Same as reorder_diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int M, int N>
void	fs_svd_errbd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > u=0, Eigen::Matrix< Scalar, N, N > v=0, Real s_errbd=0, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > u_errbd=0, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *v_errbd=0)

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &v)
	Singular value decomposition of M-by-N matrix m such that.

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &v, Real &s_errbd)
	Same as fs_svd(m, s, u, v) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< Scalar, M, M > &u, Eigen::Matrix< Scalar, N, N > &v, Real &s_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &u_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &v_errbd)
	Same as fs_svd(m, s, u, v, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s)
	Returns singular values of M-by-N matrix m via s such that `(s >= 0).all()`.

template<class Real , class Scalar , int M, int N>
void	fs_svd (const Eigen::Matrix< Scalar, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Real &s_errbd)
	Same as fs_svd(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , int M, int N>
void	fs_svd (const Eigen::Matrix< Real, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< std::complex< Real >, M, M > &u, Eigen::Matrix< std::complex< Real >, N, N > &v)
	Singular value decomposition of M-by-N real matrix m such that.

template<class Real , int M, int N>
void	fs_svd (const Eigen::Matrix< Real, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< std::complex< Real >, M, M > &u, Eigen::Matrix< std::complex< Real >, N, N > &v, Real &s_errbd)
	Same as fs_svd(m, s, u, v) except that an approximate error bound for the singular values is returned as well.

template<class Real , int M, int N>
void	fs_svd (const Eigen::Matrix< Real, M, N > &m, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &s, Eigen::Matrix< std::complex< Real >, M, M > &u, Eigen::Matrix< std::complex< Real >, N, N > &v, Real &s_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &u_errbd, Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &v_errbd)
	Same as fs_svd(m, s, u, v, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric_errbd (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > u=0, Real s_errbd=0, Eigen::Array< Real, N, 1 > *u_errbd=0)

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u)
	Diagonalizes N-by-N symmetric matrix m so that.

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd)
	Same as fs_diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Eigen::Matrix< std::complex< Real >, N, N > &u, Real &s_errbd, Eigen::Array< Real, N, 1 > &u_errbd)
	Same as fs_diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s)
	Returns singular values of N-by-N symmetric matrix m via s such that `(s >= 0).all()`.

template<class Real , class Scalar , int N>
void	fs_diagonalize_symmetric (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &s, Real &s_errbd)
	Same as fs_diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian_errbd (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > z=0, Real w_errbd=0, Eigen::Array< Real, N, 1 > *z_errbd=0)

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z)
	Diagonalizes N-by-N hermitian matrix m so that.

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd)
	Same as fs_diagonalize_hermitian(m, w, z) except that an approximate error bound for the eigenvalues is returned as well.

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Eigen::Matrix< Scalar, N, N > &z, Real &w_errbd, Eigen::Array< Real, N, 1 > &z_errbd)
	Same as fs_diagonalize_hermitian(m, w, z, w_errbd) except that approximate error bounds for the eigenvectors are returned as well.

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w)
	Returns eigenvalues of N-by-N hermitian matrix m via w.

template<class Real , class Scalar , int N>
void	fs_diagonalize_hermitian (const Eigen::Matrix< Scalar, N, N > &m, Eigen::Array< Real, N, 1 > &w, Real &w_errbd)
	Same as fs_diagonalize_hermitian(m, w) except that an approximate error bound for the eigenvalues is returned as well.

double	calculate_mb_SM5_DRbar (double mb_mb, double alpha_s, double scale)
	Calculates mb(Q) in the DR-bar scheme in the SM w/ 5 active quark flavours using the approach described in arxiv:hep-ph/0207126 .

double	calculate_mt_SM6_MSbar (double mt_pole, double alpha_s_mz, double mz, double scale) noexcept
	Calculates the running top quark MS-bar mass mt(SM(6),Q) at the scale Q.

double	calculate_mb_SM6_MSbar (double mb_mb, double mt_pole, double alpha_s_mz, double mz, double scale) noexcept
	Calculates the running bottom quark MS-bar mass mb(SM(6),Q) in the SM(6) at the scale Q.

double	calculate_mtau_SM6_MSbar (double mtau_pole, double alpha_em_mz, double scale) noexcept
	Calculates the running tau lepton MS-bar mass mtau(SM(6),Q) in the SM(6) at the scale Q.

double	abs_sqrt (double) noexcept
	returns square root of absolute of number

int	sign (double) noexcept
	returns sign of real number

double	signed_sqr (double) noexcept
	returns square of number, times sign

double	signed_abs_sqrt (double) noexcept
	returns square root of absolute of number, times sign

template<typename T >
T	sqr (T x) noexcept
	returns number squared

template<typename T >
T	cube (T x) noexcept
	returns number to the third power

template<typename T >
T	pow3 (T x) noexcept
	returns number to the third power

template<typename T >
T	pow4 (T x) noexcept
	returns number to the 4th power

template<typename T >
bool	is_zero (T a, T eps) noexcept

template<typename T >
bool	is_equal (T a, T b, T eps) noexcept

template<typename T >
bool	is_equal_rel (T a, T b, T eps) noexcept

template<typename T >
constexpr RAII_save< T >	make_raii_save (T &var)

double	calculate_uncertainty_amu_0loop (const THDM &, double, double)
	calculates uncertainty for amu(0-loop)

double	calculate_uncertainty_amu_1loop (const THDM &, double, double)
	calculates uncertainty for amu(1-loop)

double	calculate_uncertainty_amu_2loop (const THDM &, double, double)
	calculates uncertainty for amu(2-loop)

double	calculate_uncertainty_amu_0loop (const MSSMNoFV_onshell &, double)
	calculates uncertainty for amu(0-loop) w/ tan(beta) resummation

double	calculate_uncertainty_amu_1loop (const MSSMNoFV_onshell &, double)
	calculates uncertainty for amu(1-loop) w/ tan(beta) resummation

double	calculate_amu_1loop_non_tan_beta_resummed (const MSSMNoFV_onshell &model)
	Calculates full 1-loop SUSY contribution to (g-2), Eq (45) of arXiv:hep-ph/0609168.

double	calculate_amu_1loop (const MSSMNoFV_onshell &model)
	Calculates full 1-loop SUSY contribution to (g-2), Eq (45) of arXiv:hep-ph/0609168.

double	amu1LChi0 (const MSSMNoFV_onshell &model)
	Calculates 1-loop neutralino contribution to (g-2), Eq (2.11a) of arXiv:1311.1775.

double	amu1LChipm (const MSSMNoFV_onshell &model)
	Calculates 1-loop chargino contribution to (g-2), Eq (2.11b) of arXiv:1311.1775.

Eigen::Array< std::complex< double >, 4, 2 >	n_L (const MSSMNoFV_onshell &model)
	Calculates $n^L_{i\tilde{l}_k}$ , Eq (2.5o) of arXiv:1311.1775, for $l=\mu$ .

Eigen::Array< std::complex< double >, 4, 2 >	n_R (const MSSMNoFV_onshell &model)
	Calculates $n^R_{i\tilde{l}_k}$ , Eq (2.5p) of arXiv:1311.1775, with $l=\mu$ .

Eigen::Array< std::complex< double >, 2, 1 >	c_L (const MSSMNoFV_onshell &model)
	Calculates $c^L_{i\tilde{\nu}_\mu}$ , Eq (2.5a) of arXiv:1311.1775 for $l=\mu$ .

Eigen::Array< std::complex< double >, 2, 1 >	c_R (const MSSMNoFV_onshell &model)
	Calculates $c^R_{i\tilde{\nu}_\mu}$ , Eq (2.5b) of arXiv:1311.1775 for $l=\mu$ .

Eigen::Array< double, 2, 1 >	AAC (const MSSMNoFV_onshell &model)
	Calculates $\mathcal{A}^{c+}_{ii\tilde{\nu}_\mu} = \|c^L_{i\tilde{\nu}_\mu}\|^2 + \|c^R_{i\tilde{\nu}_\mu}\|^2$ , Eqs (2.11b), (2.7a) in arXiv:1311.1775.

Eigen::Array< double, 4, 2 >	AAN (const MSSMNoFV_onshell &model)
	Calculates $\mathcal{A}^{n+}_{ii\tilde{\mu}_m} = \|n^L_{i\tilde{\mu}_m}\|^2 + \|n^R_{i\tilde{\mu}_m}\|^2$ , Eqs (2.11a), (2.7a) in arXiv:1311.1775.

Eigen::Array< double, 2, 1 >	BBC (const MSSMNoFV_onshell &model)
	Calculates $\mathcal{B}^{c+}_{ii\tilde{\nu}_\mu} = 2 \text{Re} [(c^L_{i\tilde{\nu}_\mu})^* c^R_{i\tilde{\nu}_\mu}]$ , Eqs (2.11b), (2.7b) in arXiv:1311.1775.

Eigen::Array< double, 4, 2 >	BBN (const MSSMNoFV_onshell &model)
	Calculates $\mathcal{B}^{n+}_{ii\tilde{\mu}_m} = 2 \text{Re} [(n^L_{i\tilde{\mu}_m})^* n^R_{i\tilde{\mu}_m}]$ , Eqs (2.11a), (2.7b) in arXiv:1311.1775.

Eigen::Array< double, 4, 2 >	x_im (const MSSMNoFV_onshell &model)
	Calculates $x_{im} = m^2_{\chi_i^0} / m^2_{\tilde{\mu}_m}$ , which appears in Eq (46) of arXiv:hep-ph/0609168.

Eigen::Array< double, 2, 1 >	x_k (const MSSMNoFV_onshell &model)
	Calculates $x_k = m^2_{\chi_k^\pm} / m^2_{\tilde{\nu}_\mu}$ , which appears in Eq (47) of arXiv:hep-ph/0609168.

double	amu1LWHnu (const MSSMNoFV_onshell &model)
	Calculates the 1-loop leading log approximation: Wino–Higgsino, muon-sneutrino, Eq (6.2a) arXiv:1311.1775.

double	amu1LWHmuL (const MSSMNoFV_onshell &model)
	Calculates the 1-loop leading log approximation: Wino–Higgsino, left-handed smuon, Eq (6.2b) arXiv:1311.1775.

double	amu1LBHmuL (const MSSMNoFV_onshell &model)
	Calculates the 1-loop leading log approximation: Bino–Higgsino, left-handed smuon, Eq (6.2c) arXiv:1311.1775.

double	amu1LBHmuR (const MSSMNoFV_onshell &model)
	Calculates the 1-loop leading log approximation: Bino–Higgsino, right-handed smuon, Eq (6.2d) arXiv:1311.1775.

double	amu1LBmuLmuR (const MSSMNoFV_onshell &model)
	Calculates the 1-loop leading log approximation: Bino, left-handed smuon, right-handed smuon, Eq (6.2e) arXiv:1311.1775.

double	amu1Lapprox_non_tan_beta_resummed (const MSSMNoFV_onshell &model)
	Calculates the full 1-loop leading log approximation, Eq (6.1) arXiv:1311.1775 as it stands, without tan(beta) resummation.

double	amu1Lapprox (const MSSMNoFV_onshell &model)
	Calculates the full 1-loop leading log approximation, Eq (6.1) arXiv:1311.1775 but include tan(beta) resummation.

double	tan_beta_cor (const MSSMNoFV_onshell &model)
	Calculates $\frac{1}{1 + \Delta_{\mu}}$ .

double	delta_down_lepton_correction (const MSSMNoFV_onshell &model, int gen)
	Calculates $\Delta_{\ell}$ using a generalized form of Eq (8) arxiv:0808.1530.

double	delta_mu_correction (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{\mu}$ using delta_down_lepton_correction()

double	delta_tau_correction (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{\tau}$ using delta_down_lepton_correction()

double	delta_bottom_correction (const MSSMNoFV_onshell &model)
	Returns the $\Delta_b$ corrections from arxiv:0901.2065, Eq (103) and Eqs (31)-(35)

double	calculate_amu_2loop_non_tan_beta_resummed (const MSSMNoFV_onshell &model)
	Calculates best 2-loop SUSY contribution to a_mu without tan(beta) resummation.

double	calculate_amu_2loop (const MSSMNoFV_onshell &model)
	Calculates best 2-loop SUSY contribution to a_mu with tan(beta) resummation.

double	log_scale (const MSSMNoFV_onshell &model)
	Calculates $m_{SUSY}$ , p.37 arxiv:1311.1775.

double	delta_g1 (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{g_1}$ , Eq (6.6a) arxiv:1311.1775.

double	delta_yuk_higgsino (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{\tilde{H}}$ , Eq (6.6c) arxiv:1311.1775.

double	delta_yuk_bino_higgsino (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{\tilde{B}\tilde{H}}$ , Eq (6.6d) arxiv:1311.1775.

double	delta_g2 (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{g_2}$ , Eq (6.6b) arxiv:1311.1775.

double	delta_yuk_wino_higgsino (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{\tilde{W}\tilde{H}}$ , Eq (6.6e) arxiv:1311.1775.

double	delta_tan_beta (const MSSMNoFV_onshell &model)
	Calculates $\Delta_{t_\beta}$ , Eq (6.6f) arxiv:1311.1775.

double	amu2LWHnu (const MSSMNoFV_onshell &model)
	Calculates 1st line of Eq (6.5) arxiv:1311.1775.

double	amu2LWHmuL (const MSSMNoFV_onshell &model)
	Calculates 2nd line of Eq (6.5) arxiv:1311.1775.

double	amu2LBHmuL (const MSSMNoFV_onshell &model)
	Calculates 3rd line of Eq (6.5) arxiv:1311.1775.

double	amu2LBHmuR (const MSSMNoFV_onshell &model)
	Calculates 4th line of Eq (6.5) arxiv:1311.1775.

double	amu2LBmuLmuR (const MSSMNoFV_onshell &model)
	Calculates 5th line of Eq (6.5) arxiv:1311.1775.

double	amu2LFSfapprox_non_tan_beta_resummed (const MSSMNoFV_onshell &model)
	Calculates 2-loop leading log approximation for fermion-sfermion loop contributions, Eq (6.5) arxiv:1311.1775.

double	amu2LFSfapprox (const MSSMNoFV_onshell &model)
	Calculates 2-loop leading log approximation for fermion-sfermion loop contributions, Eq (6.5) arxiv:1311.1775.

double	amu2LChipmPhotonic (const MSSMNoFV_onshell &model)
	Calculates the photonic 2-loop contribution to the 1-loop chargino diagram, Eq (35) arXiv:1003.5820.

double	amu2LChi0Photonic (const MSSMNoFV_onshell &model)
	Calculates the photonic 2-loop contribution to the 1-loop neutralino diagram, Eq (36) arXiv:1003.5820.

double	tan_alpha (const MSSMNoFV_onshell &model)
	The following functions include resummation of 1/(1 + Delta_mu) within the muon, tau and bottom Yukawa couplings.

Eigen::Matrix< std::complex< double >, 3, 3 >	lambda_mu_cha (const MSSMNoFV_onshell &model)
	Calculates $\lambda_{\mu}$ , Eq (65), and $\lambda_{\chi_k^+}$ , Eq (66) arXiv:hep-ph/0609168.

Eigen::Matrix< std::complex< double >, 2, 2 >	lambda_stop (const MSSMNoFV_onshell &model)
	Calculates $\lambda_{\tilde{t}_i}$ , Eq (67) arXiv:hep-ph/0609168.

Eigen::Matrix< std::complex< double >, 2, 2 >	lambda_sbot (const MSSMNoFV_onshell &model)
	Calculates $\lambda_{\tilde{b}_i}$ , Eq (68) arXiv:hep-ph/0609168.

Eigen::Matrix< std::complex< double >, 2, 2 >	lambda_stau (const MSSMNoFV_onshell &model)
	Calculates $\lambda_{\tilde{\tau}_i}$ , Eq (69) arXiv:hep-ph/0609168.

double	amu2LaSferm (const MSSMNoFV_onshell &model)
	Calculates 2-loop contribution to amu, where a sfermion loop has been inserted into a 1-loop Standard Model diagram (photonic Barr-Zee diagram $(\tilde{f}\gamma H)$ ), Eq (64) arXiv:hep-ph/0609168.

double	amu2LaCha (const MSSMNoFV_onshell &model)
	Calculates 2-loop contribution to amu, where a chargino loop has been inserted into a 1-loop Standard Model diagram (photonic Barr-Zee diagram $(\chi\gamma H)$ ), Eq (63) arXiv:hep-ph/0609168.

double	calculate_uncertainty_amu_0loop (const MSSMNoFV_onshell &model)
	Calculates uncertainty associated with amu(0-loop) including tan(beta) resummation.

double	calculate_uncertainty_amu_1loop (const MSSMNoFV_onshell &model)
	Calculates uncertainty associated with amu(1-loop) including tan(beta) resummation.

double	calculate_uncertainty_amu_2loop (const MSSMNoFV_onshell &model)
	Calculates uncertainty associated with amu(2-loop) using Eq (4).

std::ostream &	operator<< (std::ostream &, const MSSMNoFV_onshell &)
	streaming operator

std::ostream &	operator<< (std::ostream &ostr, const MSSMNoFV_onshell_mass_eigenstates &model)

std::ostream &	operator<< (std::ostream &ostr, const MSSMNoFV_onshell_physical &phys_pars)

std::ostream &	operator<< (std::ostream &ostr, const MSSMNoFV_onshell_problems &problems)

std::ostream &	operator<< (std::ostream &ostr, const MSSMNoFV_onshell_soft_parameters &soft_pars)

std::ostream &	operator<< (std::ostream &ostr, const MSSMNoFV_onshell_susy_parameters &susy_pars)

std::ostream &	operator<< (std::ostream &, const SM &)
	streaming operator

double	calculate_amu_1loop (const THDM &model)
	Calculates full 1-loop contribution to a_mu in the general THDM.

double	calculate_amu_2loop_bosonic (const THDM &model)
	Calculates 2-loop bosonic contribution to a_mu in the THDM.

double	calculate_amu_2loop_fermionic (const THDM &model)
	Calculates fermionic 2-loop contribution to a_mu in the THDM.

double	calculate_amu_2loop (const THDM &model)
	Calculates full 2-loop contribution to a_mu in the general THDM.

double	calculate_uncertainty_amu_0loop (const THDM &model)
	Calculates uncertainty associated with amu(0-loop)

double	calculate_uncertainty_amu_1loop (const THDM &model)
	Calculates uncertainty associated with amu(1-loop)

double	calculate_uncertainty_amu_2loop (const THDM &model)
	Calculates uncertainty associated with amu(2-loop)

std::ostream &	operator<< (std::ostream &, const THDM &)
	streaming operator

std::ostream &	operator<< (std::ostream &ostr, const THDM_mass_eigenstates &model)

std::ostream &	operator<< (std::ostream &ostr, const THDM_parameters &pars)

std::ostream &	operator<< (std::ostream &ostr, const THDM_problems &problems)

Variables
constexpr double	ALPHA_EM_THOMPSON = 1.0/137.035999084

constexpr double	DELTA_ALPHA_EM_MZ

constexpr double	ALPHA_EM_MZ = ALPHA_EM_THOMPSON / (1 - DELTA_ALPHA_EM_MZ)

constexpr double	ALPHA_S_MZ = 0.1184

constexpr double	MH = 125.09

constexpr double	MW = 80.385

constexpr double	MZ = 91.1876

constexpr double	MU = 0.0022

constexpr double	MC = 1.28

constexpr double	MT = 173.34

constexpr double	MD = 0.0047

constexpr double	MS = 0.096

constexpr double	MBMB = 4.18

constexpr double	ME = 0.000510998928

constexpr double	MM = 0.1056583715

constexpr double	ML = 1.777

constexpr double	CKM_THETA12 = 0.229206

constexpr double	CKM_THETA13 = 0.003960

constexpr double	CKM_THETA23 = 0.042223

constexpr double	CKM_DELTA = 0

Function Documentation

◆ AAC()

Eigen::Array< double, 2, 1 > gm2calc::AAC ( const MSSMNoFV_onshell & model )

Calculates 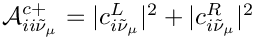$\mathcal{A}^{c+}_{ii\tilde{\nu}_\mu} = |c^L_{i\tilde{\nu}_\mu}|^2 + |c^R_{i\tilde{\nu}_\mu}|^2$ , Eqs (2.11b), (2.7a) in arXiv:1311.1775.

This expression is identical to 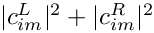$|c^L_{im}|^2 + |c^R_{im}|^2$ , which appears in Eq. (47) of arXiv:hep-ph/0609168.

Definition at line 207 of file gm2_1loop.cpp.

◆ AAN()

Eigen::Array< double, 4, 2 > gm2calc::AAN ( const MSSMNoFV_onshell & model )

Calculates 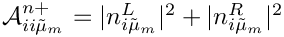$\mathcal{A}^{n+}_{ii\tilde{\mu}_m} = |n^L_{i\tilde{\mu}_m}|^2 + |n^R_{i\tilde{\mu}_m}|^2$ , Eqs (2.11a), (2.7a) in arXiv:1311.1775.

This expression is identical to 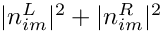$|n^L_{im}|^2 + |n^R_{im}|^2$ , which appears in Eq. (46) of arXiv:hep-ph/0609168.

Definition at line 220 of file gm2_1loop.cpp.

◆ abs_sqrt()

double gm2calc::abs_sqrt ( double x )

noexcept

returns square root of absolute of number

Definition at line 23 of file gm2_numerics.cpp.

◆ amu1Lapprox()

double gm2calc::amu1Lapprox ( const MSSMNoFV_onshell & model )

Calculates the full 1-loop leading log approximation, Eq (6.1) arXiv:1311.1775 but include tan(beta) resummation.

1-loop leading log approximation

Definition at line 372 of file gm2_1loop.cpp.

◆ amu1Lapprox_non_tan_beta_resummed()

double gm2calc::amu1Lapprox_non_tan_beta_resummed ( const MSSMNoFV_onshell & model )

Calculates the full 1-loop leading log approximation, Eq (6.1) arXiv:1311.1775 as it stands, without tan(beta) resummation.

1-loop leading log approximation w/o explicit tan(beta) resummation

Definition at line 361 of file gm2_1loop.cpp.

◆ amu1LBHmuL()

double gm2calc::amu1LBHmuL ( const MSSMNoFV_onshell & model )

Calculates the 1-loop leading log approximation: Bino–Higgsino, left-handed smuon, Eq (6.2c) arXiv:1311.1775.

1-loop bino–Higgsino, left-handed smuon leading log approximation

Definition at line 304 of file gm2_1loop.cpp.

◆ amu1LBHmuR()

double gm2calc::amu1LBHmuR ( const MSSMNoFV_onshell & model )

Calculates the 1-loop leading log approximation: Bino–Higgsino, right-handed smuon, Eq (6.2d) arXiv:1311.1775.

1-loop bino–Higgsino, right-handed smuon leading log approximation

Definition at line 321 of file gm2_1loop.cpp.

◆ amu1LBmuLmuR()

double gm2calc::amu1LBmuLmuR ( const MSSMNoFV_onshell & model )

Calculates the 1-loop leading log approximation: Bino, left-handed smuon, right-handed smuon, Eq (6.2e) arXiv:1311.1775.

1-loop bino, left-handed smuon–right-handed smuon leading log approximation

Definition at line 338 of file gm2_1loop.cpp.

◆ amu1LChi0()

double gm2calc::amu1LChi0 ( const MSSMNoFV_onshell & model )

Calculates 1-loop neutralino contribution to (g-2), Eq (2.11a) of arXiv:1311.1775.

1-loop neutralino contribution

Definition at line 83 of file gm2_1loop.cpp.

◆ amu1LChipm()

double gm2calc::amu1LChipm ( const MSSMNoFV_onshell & model )

Calculates 1-loop chargino contribution to (g-2), Eq (2.11b) of arXiv:1311.1775.

1-loop chargino contribution

Definition at line 108 of file gm2_1loop.cpp.

◆ amu1LWHmuL()

double gm2calc::amu1LWHmuL ( const MSSMNoFV_onshell & model )

Calculates the 1-loop leading log approximation: Wino–Higgsino, left-handed smuon, Eq (6.2b) arXiv:1311.1775.

1-loop wino–Higgsino, left-handed smuon leading log approximation

Definition at line 288 of file gm2_1loop.cpp.

◆ amu1LWHnu()

double gm2calc::amu1LWHnu ( const MSSMNoFV_onshell & model )

Calculates the 1-loop leading log approximation: Wino–Higgsino, muon-sneutrino, Eq (6.2a) arXiv:1311.1775.

1-loop wino–Higgsino, muon-sneutrino leading log approximation

Definition at line 272 of file gm2_1loop.cpp.

◆ amu2LaCha()

double gm2calc::amu2LaCha ( const MSSMNoFV_onshell & model )

Calculates 2-loop contribution to amu, where a chargino loop has been inserted into a 1-loop Standard Model diagram (photonic Barr-Zee diagram 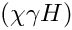$(\chi\gamma H)$ ), Eq (63) arXiv:hep-ph/0609168.

2-loop 2L(a) chargino/neutralino contribution

Definition at line 635 of file gm2_2loop.cpp.

◆ amu2LaSferm()

double gm2calc::amu2LaSferm ( const MSSMNoFV_onshell & model )

Calculates 2-loop contribution to amu, where a sfermion loop has been inserted into a 1-loop Standard Model diagram (photonic Barr-Zee diagram 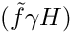$(\tilde{f}\gamma H)$ ), Eq (64) arXiv:hep-ph/0609168.

2-loop 2L(a) sfermion contribution

Definition at line 584 of file gm2_2loop.cpp.

◆ amu2LBHmuL()

double gm2calc::amu2LBHmuL ( const MSSMNoFV_onshell & model )

Calculates 3rd line of Eq (6.5) arxiv:1311.1775.

Definition at line 285 of file gm2_2loop.cpp.

◆ amu2LBHmuR()

double gm2calc::amu2LBHmuR ( const MSSMNoFV_onshell & model )

Calculates 4th line of Eq (6.5) arxiv:1311.1775.

Definition at line 296 of file gm2_2loop.cpp.

◆ amu2LBmuLmuR()

double gm2calc::amu2LBmuLmuR ( const MSSMNoFV_onshell & model )

Calculates 5th line of Eq (6.5) arxiv:1311.1775.

Definition at line 307 of file gm2_2loop.cpp.

◆ amu2LChi0Photonic()

double gm2calc::amu2LChi0Photonic ( const MSSMNoFV_onshell & model )

Calculates the photonic 2-loop contribution to the 1-loop neutralino diagram, Eq (36) arXiv:1003.5820.

2-loop photonic neutralino contribution

Definition at line 383 of file gm2_2loop.cpp.

◆ amu2LChipmPhotonic()

double gm2calc::amu2LChipmPhotonic ( const MSSMNoFV_onshell & model )

Calculates the photonic 2-loop contribution to the 1-loop chargino diagram, Eq (35) arXiv:1003.5820.

2-loop photonic chargino contribution

Definition at line 350 of file gm2_2loop.cpp.

◆ amu2LFSfapprox()

double gm2calc::amu2LFSfapprox ( const MSSMNoFV_onshell & model )

Calculates 2-loop leading log approximation for fermion-sfermion loop contributions, Eq (6.5) arxiv:1311.1775.

2-loop fermion/sfermion contribution (approximation)

Includes tan(beta) resummation

Definition at line 339 of file gm2_2loop.cpp.

◆ amu2LFSfapprox_non_tan_beta_resummed()

double gm2calc::amu2LFSfapprox_non_tan_beta_resummed ( const MSSMNoFV_onshell & model )

Calculates 2-loop leading log approximation for fermion-sfermion loop contributions, Eq (6.5) arxiv:1311.1775.

2-loop fermion/sfermion contribution (approximation) w/o tan(beta) resummation

No tan(beta) resummation

Definition at line 318 of file gm2_2loop.cpp.

◆ amu2LWHmuL()

double gm2calc::amu2LWHmuL ( const MSSMNoFV_onshell & model )

Calculates 2nd line of Eq (6.5) arxiv:1311.1775.

Definition at line 274 of file gm2_2loop.cpp.

◆ amu2LWHnu()

double gm2calc::amu2LWHnu ( const MSSMNoFV_onshell & model )

Calculates 1st line of Eq (6.5) arxiv:1311.1775.

Definition at line 263 of file gm2_2loop.cpp.

◆ BBC()

Eigen::Array< double, 2, 1 > gm2calc::BBC ( const MSSMNoFV_onshell & model )

Calculates $\mathcal{B}^{c+}_{ii\tilde{\nu}_\mu} = 2 \text{Re} [(c^L_{i\tilde{\nu}_\mu})^* c^R_{i\tilde{\nu}_\mu}]$ , Eqs (2.11b), (2.7b) in arXiv:1311.1775.

Definition at line 230 of file gm2_1loop.cpp.

◆ BBN()

Eigen::Array< double, 4, 2 > gm2calc::BBN ( const MSSMNoFV_onshell & model )

Calculates $\mathcal{B}^{n+}_{ii\tilde{\mu}_m} = 2 \text{Re} [(n^L_{i\tilde{\mu}_m})^* n^R_{i\tilde{\mu}_m}]$ , Eqs (2.11a), (2.7b) in arXiv:1311.1775.

Definition at line 240 of file gm2_1loop.cpp.

◆ c_L()

Eigen::Array< std::complex< double >, 2, 1 > gm2calc::c_L ( const MSSMNoFV_onshell & model )

Calculates 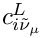$c^L_{i\tilde{\nu}_\mu}$ , Eq (2.5a) of arXiv:1311.1775 for $l=\mu$ .

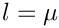
This expression is the complex conjugate of Eq. (50) of arXiv:hep-ph/0609168.

Definition at line 183 of file gm2_1loop.cpp.

◆ c_R()

Eigen::Array< std::complex< double >, 2, 1 > gm2calc::c_R ( const MSSMNoFV_onshell & model )

Calculates 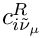$c^R_{i\tilde{\nu}_\mu}$ , Eq (2.5b) of arXiv:1311.1775 for $l=\mu$ .

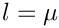
This expression is equal to Eq. (51) of arXiv:hep-ph/0609168.

Definition at line 194 of file gm2_1loop.cpp.

◆ calculate_amu_1loop() [1/2]

double gm2calc::calculate_amu_1loop ( const MSSMNoFV_onshell & model )

Calculates full 1-loop SUSY contribution to (g-2), Eq (45) of arXiv:hep-ph/0609168.

calculates full 1-loop SUSY contributions to (g-2) in the MSSM (w/ tan(beta) resummation)

This function assumes that the Yukawa coupling is defined according to arXiv:1504.05500, Eq. (13) and footnote 2. Therefore, this function uses tan(beta) resummation in the Yukawa coupling.

Definition at line 74 of file gm2_1loop.cpp.

◆ calculate_amu_1loop() [2/2]

double gm2calc::calculate_amu_1loop ( const THDM & model )

Calculates full 1-loop contribution to a_mu in the general THDM.

calculates full 1-loop contributions to a_mu in the general THDM

Parameters

model THDM model parameters, masses and mixings

Returns: 1-loop contribution to a_mu

Definition at line 39 of file gm2_1loop.cpp.

◆ calculate_amu_1loop_non_tan_beta_resummed()

double gm2calc::calculate_amu_1loop_non_tan_beta_resummed ( const MSSMNoFV_onshell & model )

Calculates full 1-loop SUSY contribution to (g-2), Eq (45) of arXiv:hep-ph/0609168.

calculates full 1-loop SUSY contributions to (g-2) in the MSSM (no tan(beta) resummation)

This function re-defines the muon Yukawa coupling in terms of the tree-level relation with the muon pole mass, i.e. 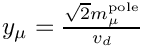$y_\mu = \frac{\sqrt{2} m_\mu^\text{pole}}{v_d}$ . Therefore, this function does not use tan(beta) resummation.

Definition at line 57 of file gm2_1loop.cpp.

◆ calculate_amu_2loop() [1/2]

double gm2calc::calculate_amu_2loop ( const MSSMNoFV_onshell & model )

Calculates best 2-loop SUSY contribution to a_mu with tan(beta) resummation.

calculates best 2-loop SUSY contributions to a_mu in the MSSM (with tan(beta) resummation)

Definition at line 111 of file gm2_2loop.cpp.

◆ calculate_amu_2loop() [2/2]

double gm2calc::calculate_amu_2loop ( const THDM & model )

Calculates full 2-loop contribution to a_mu in the general THDM.

calculates full 2-loop contributions to a_mu in the general THDM

Parameters

model THDM model parameters, masses and mixings

Returns: 2-loop contribution to a_mu

Definition at line 94 of file gm2_2loop.cpp.

◆ calculate_amu_2loop_bosonic()

double gm2calc::calculate_amu_2loop_bosonic ( const THDM & model )

Calculates 2-loop bosonic contribution to a_mu in the THDM.

calculates bosonic 2-loop contributions to a_mu in the general THDM

Parameters

model THDM model parameters, masses and mixings

Returns: 2-loop contribution to a_mu

Definition at line 31 of file gm2_2loop.cpp.

◆ calculate_amu_2loop_fermionic()

double gm2calc::calculate_amu_2loop_fermionic ( const THDM & model )

Calculates fermionic 2-loop contribution to a_mu in the THDM.

calculates fermionic 2-loop contributions to a_mu in the general THDM

Parameters

model THDM model parameters, masses and mixings

Returns: 2-loop contribution to a_mu

Definition at line 57 of file gm2_2loop.cpp.

◆ calculate_amu_2loop_non_tan_beta_resummed()

double gm2calc::calculate_amu_2loop_non_tan_beta_resummed ( const MSSMNoFV_onshell & model )

Calculates best 2-loop SUSY contribution to a_mu without tan(beta) resummation.

calculates best 2-loop SUSY contributions to a_mu in the MSSM (no tan(beta) resummation)

This function re-defines the muon Yukawa coupling in terms of the tree-level relation with the muon pole mass, i.e. 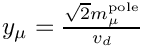$y_\mu = \frac{\sqrt{2} m_\mu^\text{pole}}{v_d}$ . Therefore, this function does not use tan(beta) resummation.

Definition at line 95 of file gm2_2loop.cpp.

◆ calculate_mb_SM5_DRbar()

double gm2calc::calculate_mb_SM5_DRbar	(	double	mb_mb,
		double	alpha_s,
		double	scale
	)

Calculates mb(Q) in the DR-bar scheme in the SM w/ 5 active quark flavours using the approach described in arxiv:hep-ph/0207126 .

calculates mb(Q) DR-bar

Parameters

mb_mb	mb(mb) MS-bar in SM w/ 5 active quark flavours
alpha_s	alpha_s MS-bar in SM w/ 5 quark flavours at scale Q
scale	renormalization scale Q

Returns: mb(Q) DR-bar in the SM w/ 5 quarks

Definition at line 202 of file gm2_mf.cpp.

◆ calculate_mb_SM6_MSbar()

double gm2calc::calculate_mb_SM6_MSbar	(	double	mb_mb,
		double	mt_pole,
		double	alpha_s_mz,
		double	mz,
		double	scale
	)

noexcept

Calculates the running bottom quark MS-bar mass mb(SM(6),Q) in the SM(6) at the scale Q.

calculates mb(Q) MS-bar in the SM(6)

Parameters

mb_mb	bottom quark MS-bar mass mb(mb) in the SM(5)
mt_pole	top quark pole mass
alpha_s_mz	strong coupling at the scale mz
mz	Z boson pole mass
scale	renormalization scale

Returns: mb(MS-bar,SM(6),Q)

Definition at line 262 of file gm2_mf.cpp.

◆ calculate_mt_SM6_MSbar()

double gm2calc::calculate_mt_SM6_MSbar	(	double	mt_pole,
		double	alpha_s_mz,
		double	mz,
		double	scale
	)

noexcept

Calculates the running top quark MS-bar mass mt(SM(6),Q) at the scale Q.

calculates mt(Q) MS-bar in the SM(6)

Parameters

mt_pole	top quark pole mass
alpha_s_at_mz	strong coupling at the scale Q = mz
mz	Z boson pole mass
scale	renormalization scale

Returns: mt(SM(6),MS-bar,Q)

Definition at line 232 of file gm2_mf.cpp.

◆ calculate_mtau_SM6_MSbar()

double gm2calc::calculate_mtau_SM6_MSbar	(	double	mtau_pole,
		double	alpha_em_mz,
		double	scale
	)

noexcept

Calculates the running tau lepton MS-bar mass mtau(SM(6),Q) in the SM(6) at the scale Q.

calculates mtau(Q) MS-bar in the SM(6)

Parameters

mtau_pole	tau lepton pole mass
alpha_em_mz	electromagnetic coupling at the scale Q = MZ
scale	renormalization scale

Returns: mtau(MS-bar,SM(6),Q)

Definition at line 293 of file gm2_mf.cpp.

◆ calculate_uncertainty_amu_0loop() [1/4]

double gm2calc::calculate_uncertainty_amu_0loop	(	const MSSMNoFV_onshell &	,
		double	amu_1L
	)

calculates uncertainty for amu(0-loop) w/ tan(beta) resummation

Calculates uncertainty associated with amu(0-loop) including tan(beta) resummation.

The estimated uncertainty is the magnitude amu(1-loop) (including tan(beta) resummation).

Parameters

model	model parameters (unused tag type)
amu_1L	1-loop contribution to amu

Returns: uncertainty for amu(0-loop) w/ tan(beta) resummation

Definition at line 46 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_0loop() [2/4]

double gm2calc::calculate_uncertainty_amu_0loop ( const MSSMNoFV_onshell & model )

Calculates uncertainty associated with amu(0-loop) including tan(beta) resummation.

calculates uncertainty for amu(0-loop) w/ tan(beta) resummation

Parameters

model model parameters

Returns: uncertainty for amu(0-loop) w/ tan(beta) resummation

Definition at line 59 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_0loop() [3/4]

double gm2calc::calculate_uncertainty_amu_0loop	(	const THDM &	,
		double	amu_1L,
		double	amu_2L
	)

calculates uncertainty for amu(0-loop)

Calculates uncertainty associated with amu(0-loop)

The estimated uncertainty is the magnitude amu(1-loop) plus amu(2-loop).

Parameters

model	model parameters (unused tag type)
amu_1L	1-loop contribution to amu
amu_2L	2-loop contribution to amu

Returns: uncertainty for amu(0-loop)

Definition at line 49 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_0loop() [4/4]

double gm2calc::calculate_uncertainty_amu_0loop ( const THDM & model )

Calculates uncertainty associated with amu(0-loop)

calculates uncertainty for amu(0-loop)

Parameters

model model parameters

Returns: uncertainty for amu(0-loop)

Definition at line 61 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_1loop() [1/4]

double gm2calc::calculate_uncertainty_amu_1loop	(	const MSSMNoFV_onshell &	model,
		double	amu_2L
	)

calculates uncertainty for amu(1-loop) w/ tan(beta) resummation

Calculates uncertainty associated with amu(1-loop) including tan(beta) resummation.

The estimated uncertainty is the sum of magnitude amu(2-loop) (including tan(beta) resummation) and the 2-loop uncertainty.

Parameters

model	model parameters
amu_2L	2-loop contribution to amu

Returns: uncertainty for amu(1-loop) w/ tan(beta) resummation

Definition at line 78 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_1loop() [2/4]

double gm2calc::calculate_uncertainty_amu_1loop ( const MSSMNoFV_onshell & model )

Calculates uncertainty associated with amu(1-loop) including tan(beta) resummation.

calculates uncertainty for amu(1-loop) w/ tan(beta) resummation

Parameters

model model parameters

Returns: uncertainty for amu(1-loop) w/ tan(beta) resummation

Definition at line 93 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_1loop() [3/4]

double gm2calc::calculate_uncertainty_amu_1loop	(	const THDM &	model,
		double	amu_1L,
		double	amu_2L
	)

calculates uncertainty for amu(1-loop)

Calculates uncertainty associated with amu(1-loop)

The estimated uncertainty is the sum of magnitude amu(2-loop) and the 2-loop uncertainty, calculated by calculate_uncertainty_amu_2loop().

Parameters

model	model parameters
amu_1L	1-loop contribution to amu
amu_2L	2-loop contribution to amu

Returns: uncertainty for amu(1-loop)

Definition at line 82 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_1loop() [4/4]

double gm2calc::calculate_uncertainty_amu_1loop ( const THDM & model )

Calculates uncertainty associated with amu(1-loop)

calculates uncertainty for amu(1-loop)

Parameters

model model parameters

Returns: uncertainty for amu(1-loop)

Definition at line 96 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_2loop() [1/3]

double gm2calc::calculate_uncertainty_amu_2loop ( const MSSMNoFV_onshell & model )

Calculates uncertainty associated with amu(2-loop) using Eq (4).

calculates uncertainty for amu(2-loop)

Eq. (4) takes into account the unknown two-loop contributions and the employed approximation for the 2L(a) contributions.

Parameters

model model parameters

Returns: uncertainty for amu(2-loop)

Definition at line 110 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_2loop() [2/3]

double gm2calc::calculate_uncertainty_amu_2loop	(	const THDM &	model,
		double	amu_1L,
		double	amu_2L
	)

calculates uncertainty for amu(2-loop)

Calculates uncertainty associated with amu(2-loop)

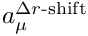
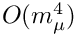
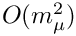
Takes into account the neglected two-loop contribution $a_\mu^{\Delta r\text{-shift}}$ , Eq.(34) arxiv:1607.06292, two-loop contributions of $O(m_\mu^4)$ and three-loop contributions of $O(m_\mu^2)$

Parameters

model	model parameters
amu_1L	1-loop contribution to amu
amu_2L	2-loop contribution to amu

Returns: uncertainty for amu(2-loop)

Definition at line 118 of file gm2_uncertainty.cpp.

◆ calculate_uncertainty_amu_2loop() [3/3]

double gm2calc::calculate_uncertainty_amu_2loop ( const THDM & model )

Calculates uncertainty associated with amu(2-loop)

calculates uncertainty for amu(2-loop)

Parameters

model model parameters

Returns: uncertainty for amu(2-loop)

Definition at line 150 of file gm2_uncertainty.cpp.

◆ clausen_2()

double gm2calc::clausen_2 ( double x )

noexcept

Clausen function 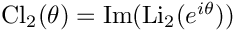$\mathrm{Cl}_2(\theta) = \mathrm{Im}(\mathrm{Li}_2(e^{i\theta}))$ .

Clausen function Cl_2(x)

Parameters

x	real angle

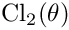
Returns: $\mathrm{Cl}_2(\theta)$

Author: Alexander Voigt

Note: Implemented as economized Padé approximation.; taken from the polylogarithm library 7.0.0

Definition at line 232 of file gm2_dilog.cpp.

◆ closest_index()

template<typename Derived >

unsigned gm2calc::closest_index	(	double	mass,
		const Eigen::ArrayBase< Derived > &	v
	)

Definition at line 29 of file gm2_eigen_utils.hpp.

◆ cube()

template<typename T >

T gm2calc::cube ( T x )

noexcept

returns number to the third power

Definition at line 32 of file gm2_numerics.hpp.

◆ delta_bottom_correction()

double gm2calc::delta_bottom_correction ( const MSSMNoFV_onshell & model )

Returns the 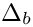$\Delta_b$ corrections from arxiv:0901.2065, Eq (103) and Eqs (31)-(35)

Definition at line 459 of file gm2_1loop.cpp.

◆ delta_down_lepton_correction()

double gm2calc::delta_down_lepton_correction	(	const MSSMNoFV_onshell &	model,
		int	gen
	)

Calculates 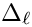$\Delta_{\ell}$ using a generalized form of Eq (8) arxiv:0808.1530.

Parameters

model	model parameters
gen	lepton generation (0 = electron, 1 = muon, 2 = tau)

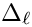
Returns: $\Delta_{\ell}$

Definition at line 402 of file gm2_1loop.cpp.

◆ delta_g1()

double gm2calc::delta_g1 ( const MSSMNoFV_onshell & model )

Calculates 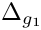$\Delta_{g_1}$ , Eq (6.6a) arxiv:1311.1775.

Contributions from 1st and 2nd generation sleptons have been included in addition.

Definition at line 141 of file gm2_2loop.cpp.

◆ delta_g2()

double gm2calc::delta_g2 ( const MSSMNoFV_onshell & model )

Calculates 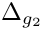$\Delta_{g_2}$ , Eq (6.6b) arxiv:1311.1775.

Contributions from 1st and 2nd generation sleptons have been included in addition.

Definition at line 215 of file gm2_2loop.cpp.

◆ delta_mu_correction()

double gm2calc::delta_mu_correction ( const MSSMNoFV_onshell & model )

Calculates 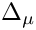$\Delta_{\mu}$ using delta_down_lepton_correction()

Parameters

model model parameters

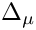
Returns: $\Delta_{\mu}$

Definition at line 438 of file gm2_1loop.cpp.

◆ delta_tan_beta()

double gm2calc::delta_tan_beta ( const MSSMNoFV_onshell & model )

Calculates 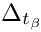$\Delta_{t_\beta}$ , Eq (6.6f) arxiv:1311.1775.

Definition at line 248 of file gm2_2loop.cpp.

◆ delta_tau_correction()

double gm2calc::delta_tau_correction ( const MSSMNoFV_onshell & model )

Calculates 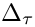$\Delta_{\tau}$ using delta_down_lepton_correction()

Parameters

model model parameters

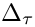
Returns: $\Delta_{\tau}$

Definition at line 450 of file gm2_1loop.cpp.

◆ delta_yuk_bino_higgsino()

double gm2calc::delta_yuk_bino_higgsino ( const MSSMNoFV_onshell & model )

Calculates 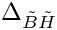$\Delta_{\tilde{B}\tilde{H}}$ , Eq (6.6d) arxiv:1311.1775.

Definition at line 197 of file gm2_2loop.cpp.

◆ delta_yuk_higgsino()

double gm2calc::delta_yuk_higgsino ( const MSSMNoFV_onshell & model )

Calculates 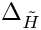$\Delta_{\tilde{H}}$ , Eq (6.6c) arxiv:1311.1775.

Definition at line 172 of file gm2_2loop.cpp.

◆ delta_yuk_wino_higgsino()

double gm2calc::delta_yuk_wino_higgsino ( const MSSMNoFV_onshell & model )

Calculates 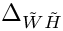$\Delta_{\tilde{W}\tilde{H}}$ , Eq (6.6e) arxiv:1311.1775.

Definition at line 235 of file gm2_2loop.cpp.

◆ diagonalize_hermitian() [1/5]

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w
	)

Returns eigenvalues of N-by-N hermitian matrix m via w.

Elements of w are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues

Definition at line 455 of file gm2_linalg.hpp.

◆ diagonalize_hermitian() [2/5]

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z
	)

Diagonalizes N-by-N hermitian matrix m so that.

m == z * w.matrix().asDiagonal() * z.adjoint()

Elements of w are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues
[out]	z	N-by-N unitary matrix

Definition at line 393 of file gm2_linalg.hpp.

◆ diagonalize_hermitian() [3/5]

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd
	)

Same as diagonalize_hermitian(m, w, z) except that an approximate error bound for the eigenvalues is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of diagonalize_hermitian(m, w, z) for the other parameters.

Definition at line 413 of file gm2_linalg.hpp.

◆ diagonalize_hermitian() [4/5]

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd,
		Eigen::Array< Real, N, 1 > &	z_errbd
	)

Same as diagonalize_hermitian(m, w, z, w_errbd) except that approximate error bounds for the eigenvectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] z_errbd array of approximate error bounds for z

See the documentation of diagonalize_hermitian(m, w, z, w_errbd) for the other parameters.

Definition at line 434 of file gm2_linalg.hpp.

◆ diagonalize_hermitian() [5/5]

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Real &	w_errbd
	)

Same as diagonalize_hermitian(m, w) except that an approximate error bound for the eigenvalues is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of diagonalize_hermitian(m, w) for the other parameters.

Definition at line 474 of file gm2_linalg.hpp.

◆ diagonalize_hermitian_errbd()

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian_errbd	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z = `0`,
		Real *	w_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	z_errbd = `0`
	)

Definition at line 355 of file gm2_linalg.hpp.

◆ diagonalize_hermitian_internal()

template<class Real , class Scalar , int N>

void gm2calc::diagonalize_hermitian_internal	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z
	)

Definition at line 346 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [1/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N real symmetric matrix m via s such that (s >= 0).all().

Order of elements of s is unspecified.

Template Parameters

Real	type of elements of m and s
N	number of rows and columns of m

Parameters

[in]	m	N-by-N real symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Note: Use diagonalize_hermitian() unless sign of s[i] matters.

Definition at line 727 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [2/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N real symmetric matrix m so that.

m == u * s.matrix().asDiagonal() * u.transpose()

and (s >= 0).all(). Order of elements of s is unspecified.

Template Parameters

Real	type of real and imaginary parts
N	number of rows and columns of m

Parameters

[in]	m	N-by-N real symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Note: Use diagonalize_hermitian() unless sign of s[i] matters.

Definition at line 663 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [3/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 683 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [4/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 704 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [5/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s) for the other parameters.

Definition at line 746 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [6/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N complex symmetric matrix m via s such that (s >= 0).all().

Elements of s are in descending order.

Template Parameters

Real	type of real and imaginary parts
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N complex symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Definition at line 592 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [7/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N complex symmetric matrix m so that.

m == u * s.matrix().asDiagonal() * u.transpose()

and (s >= 0).all(). Elements of s are in descending order.

Template Parameters

Real	type of real and imaginary parts
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N complex symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Definition at line 531 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [8/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 551 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [9/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 572 of file gm2_linalg.hpp.

◆ diagonalize_symmetric() [10/10]

template<class Real , int N>

void gm2calc::diagonalize_symmetric	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of diagonalize_symmetric(m, s) for the other parameters.

Definition at line 611 of file gm2_linalg.hpp.

◆ diagonalize_symmetric_errbd() [1/2]

template<class Real , int N>

void gm2calc::diagonalize_symmetric_errbd	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 628 of file gm2_linalg.hpp.

◆ diagonalize_symmetric_errbd() [2/2]

template<class Real , int N>

void gm2calc::diagonalize_symmetric_errbd	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 483 of file gm2_linalg.hpp.

◆ dilog() [1/2]

std::complex< double > gm2calc::dilog ( const std::complex< double > & z )

noexcept

Complex dilogarithm 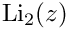$\mathrm{Li}_2(z)$ .

complex dilogarithm

Parameters

z	complex argument

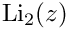
Returns: $\mathrm{Li}_2(z)$

Note: Implementation translated from SPheno to C++

Author: Werner Porod

Note: translated to C++ by Alexander Voigt; taken from the polylogarithm library 7.0.0

Definition at line 154 of file gm2_dilog.cpp.

◆ dilog() [2/2]

double gm2calc::dilog ( double x )

noexcept

Real dilogarithm 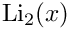$\operatorname{Li}_2(x)$ .

real dilogarithm

Parameters

x	real argument

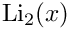
Returns: $\operatorname{Li}_2(x)$

Author: Alexander Voigt

Note: taken from the polylogarithm library 7.0.0

Implemented as an economized Pade approximation with a maximum error of 4.16e-18. [arXiv:2201.01678].

Definition at line 75 of file gm2_dilog.cpp.

◆ disna()

template<int M, int N, class Real >

void gm2calc::disna	(	const char &	JOB,
		const Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	D,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	SEP,
		int &	INFO
	)

Template version of DDISNA from LAPACK.

Definition at line 72 of file gm2_linalg.hpp.

◆ F1()

double gm2calc::F1 ( double w )

noexcept

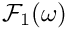
$\mathcal{F}_1(\omega)$ , Eq (25) arxiv:1502.04199

Definition at line 745 of file gm2_ffunctions.cpp.

◆ F1C()

double gm2calc::F1C ( double x )

noexcept

, Eq (54) arXiv:hep-ph/0609168

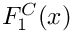
Definition at line 226 of file gm2_ffunctions.cpp.

◆ F1N()

double gm2calc::F1N ( double x )

noexcept

, Eq (52) arXiv:hep-ph/0609168

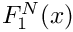
Definition at line 308 of file gm2_ffunctions.cpp.

◆ F1t()

double gm2calc::F1t ( double w )

noexcept

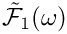
$\tilde{\mathcal{F}}_1(\omega)$ , Eq (26) arxiv:1502.04199

Definition at line 761 of file gm2_ffunctions.cpp.

◆ F2()

double gm2calc::F2 ( double w )

noexcept

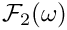
$\mathcal{F}_2(\omega)$ , Eq (27) arxiv:1502.04199

Definition at line 768 of file gm2_ffunctions.cpp.

◆ F2C()

double gm2calc::F2C ( double x )

noexcept

, Eq (55) arXiv:hep-ph/0609168

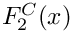
Definition at line 242 of file gm2_ffunctions.cpp.

◆ F2N()

double gm2calc::F2N ( double x )

noexcept

, Eq (53) arXiv:hep-ph/0609168

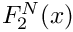
Definition at line 323 of file gm2_ffunctions.cpp.

◆ F3()

double gm2calc::F3 ( double w )

noexcept

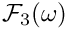
$\mathcal{F}_3(\omega)$ , Eq (28) arxiv:1502.04199

Author: Alexander Voigt

Definition at line 783 of file gm2_ffunctions.cpp.

◆ F3C()

double gm2calc::F3C ( double x )

noexcept

, Eq (37) arXiv:1003.5820

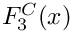
Definition at line 257 of file gm2_ffunctions.cpp.

◆ F3N()

double gm2calc::F3N ( double x )

noexcept

, Eq (39) arXiv:1003.5820

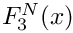
Definition at line 338 of file gm2_ffunctions.cpp.

◆ F4C()

double gm2calc::F4C ( double x )

noexcept

, Eq (38) arXiv:1003.5820

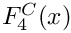
Definition at line 281 of file gm2_ffunctions.cpp.

◆ F4N()

double gm2calc::F4N ( double x )

noexcept

, Eq (40) arXiv:1003.5820

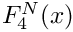
Definition at line 359 of file gm2_ffunctions.cpp.

◆ f_CSd()

double gm2calc::f_CSd	(	double	xu,
		double	xd,
		double	qu,
		double	qd
	)

noexcept

Eq (61), arxiv:1607.06292, with extra global prefactor xd.

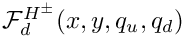
$\mathcal{F}_d^{H^\pm}(x,y,q_u,q_d)$ , Eq (61) arxiv:1607.06292

Note: There is a misprint in Eq (61), arxiv:1607.06292v2: There should be no Phi function in the 2nd line of (61).

Definition at line 699 of file gm2_ffunctions.cpp.

◆ f_CSl()

double gm2calc::f_CSl ( double z )

noexcept

Calculates Barr-Zee 2-loop function for diagram with lepton loop and charged Higgs and W boson mediators, Eq (60), arxiv:1607.06292, with extra global prefactor z.

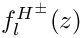
$f_l^{H^\pm}(z)$ , Eq (60) arxiv:1607.06292

Definition at line 680 of file gm2_ffunctions.cpp.

◆ f_CSu()

double gm2calc::f_CSu	(	double	xu,
		double	xd,
		double	qu,
		double	qd
	)

noexcept

Eq (62), arxiv:1607.06292, with extra global prefactor xu.

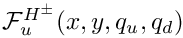
$\mathcal{F}_u^{H^\pm}(x,y,q_u,q_d)$ , Eq (62) arxiv:1607.06292

Definition at line 721 of file gm2_ffunctions.cpp.

◆ f_PS()

double gm2calc::f_PS ( double z )

noexcept

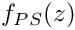
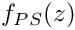
Calculates $f_{PS}(z)$ , Eq (70) arXiv:hep-ph/0609168.

$f_{PS}(z)$ , Eq (70) arXiv:hep-ph/0609168

Author: Alexander Voigt

Definition at line 616 of file gm2_ffunctions.cpp.

◆ f_S()

double gm2calc::f_S ( double z )

noexcept

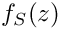
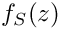
Calculates , Eq (71) arXiv:hep-ph/0609168.

, Eq (71) arXiv:hep-ph/0609168

Definition at line 645 of file gm2_ffunctions.cpp.

◆ f_sferm()

double gm2calc::f_sferm ( double z )

noexcept

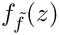
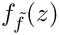
Calculates $f_{\tilde{f}}(z)$ , Eq (72) arXiv:hep-ph/0609168.

$f_{\tilde{f}}(z)$ , Eq (72) arXiv:hep-ph/0609168

Definition at line 664 of file gm2_ffunctions.cpp.

◆ Fa()

double gm2calc::Fa	(	double	x,
		double	y
	)

noexcept

, Eq (6.3a) arXiv:1311.1775

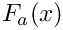
Definition at line 472 of file gm2_ffunctions.cpp.

◆ Fb()

double gm2calc::Fb	(	double	x,
		double	y
	)

noexcept

, Eq (6.3b) arXiv:1311.1775

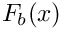
Definition at line 413 of file gm2_ffunctions.cpp.

◆ FCWd()

double gm2calc::FCWd	(	double	xu,
		double	xd,
		double	yu,
		double	yd,
		double	qu,
		double	qd
	)

noexcept

Barr-Zee 2-loop function with down-type quark loop and charge scalar and W boson mediators.

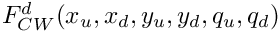
$F_{CW}^d(x_u,x_d,y_u,y_d,q_u,q_d)$

Parameters

xu	squared mass ratio (mu/ms)^2.
xd	squared mass ratio (md/ms)^2.
yu	squared mass ratio (mu/mw)^2.
yd	squared mass ratio (md/mw)^2.
qu	electric charge count of up-type quark
qd	electric charge count of down-type quark

Definition at line 941 of file gm2_ffunctions.cpp.

◆ FCWl()

double gm2calc::FCWl	(	double	x,
		double	y
	)

noexcept

Barr-Zee 2-loop function with lepton loop and charge scalar and W boson mediators.

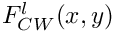
$F_{CW}^l(x,y)$

Parameters

x	squared mass ratio (mf/ms)^2.
y	squared mass ratio (mf/mw)^2.

Definition at line 879 of file gm2_ffunctions.cpp.

◆ FCWu()

double gm2calc::FCWu	(	double	xu,
		double	xd,
		double	yu,
		double	yd,
		double	qu,
		double	qd
	)

noexcept

Barr-Zee 2-loop function with up-type quark loop and charge scalar and W boson mediators.

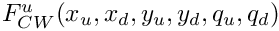
$F_{CW}^u(x_u,x_d,y_u,y_d,q_u,q_d)$

Parameters

xu	squared mass ratio (mu/ms)^2.
xd	squared mass ratio (md/ms)^2.
yu	squared mass ratio (mu/mw)^2.
yd	squared mass ratio (md/mw)^2.
qu	electric charge count of up-type quark
qd	electric charge count of down-type quark

Definition at line 912 of file gm2_ffunctions.cpp.

◆ FPZ()

double gm2calc::FPZ	(	double	x,
		double	y
	)

noexcept

Barr-Zee 2-loop function with fermion loop and pseudoscalar and Z boson mediators.

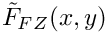
$\tilde{F}_{FZ}(x,y)$

Parameters

x	squared mass ratio (mf/ms)^2.
y	squared mass ratio (mf/mz)^2.

Definition at line 809 of file gm2_ffunctions.cpp.

◆ fs_diagonalize_hermitian() [1/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w
	)

Returns eigenvalues of N-by-N hermitian matrix m via w.

w is arranged so that abs(w[i]) are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues

Definition at line 1479 of file gm2_linalg.hpp.

◆ fs_diagonalize_hermitian() [2/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z
	)

Diagonalizes N-by-N hermitian matrix m so that.

m == z.adjoint() * w.matrix().asDiagonal() * z    // convention of SARAH

w is arranged so that abs(w[i]) are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m and z
N	number of rows and columns in m and z

Parameters

[in]	m	N-by-N matrix to be diagonalized
[out]	w	array of length N to contain eigenvalues
[out]	z	N-by-N unitary matrix

Definition at line 1417 of file gm2_linalg.hpp.

◆ fs_diagonalize_hermitian() [3/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd
	)

Same as fs_diagonalize_hermitian(m, w, z) except that an approximate error bound for the eigenvalues is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of fs_diagonalize_hermitian(m, w, z) for the other parameters.

Definition at line 1437 of file gm2_linalg.hpp.

◆ fs_diagonalize_hermitian() [4/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > &	z,
		Real &	w_errbd,
		Eigen::Array< Real, N, 1 > &	z_errbd
	)

Same as fs_diagonalize_hermitian(m, w, z, w_errbd) except that approximate error bounds for the eigenvectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] z_errbd array of approximate error bounds for z

See the documentation of fs_diagonalize_hermitian(m, w, z, w_errbd) for the other parameters.

Definition at line 1458 of file gm2_linalg.hpp.

◆ fs_diagonalize_hermitian() [5/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_hermitian	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Real &	w_errbd
	)

Same as fs_diagonalize_hermitian(m, w) except that an approximate error bound for the eigenvalues is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node89.html.

Parameters

[out] w_errbd approximate error bound for the elements of w

See the documentation of fs_diagonalize_hermitian(m, w) for the other parameters.

Definition at line 1498 of file gm2_linalg.hpp.

◆ fs_diagonalize_hermitian_errbd()

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_hermitian_errbd	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z = `0`,
		Real *	w_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	z_errbd = `0`
	)

Definition at line 1378 of file gm2_linalg.hpp.

◆ fs_diagonalize_symmetric() [1/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N symmetric matrix m via s such that (s >= 0).all().

Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Definition at line 1350 of file gm2_linalg.hpp.

◆ fs_diagonalize_symmetric() [2/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N symmetric matrix m so that.

m == u.transpose() * s.matrix().asDiagonal() * u
// convention of Haber and Kane, Phys. Rept. 117 (1985) 75-263

and (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Definition at line 1288 of file gm2_linalg.hpp.

◆ fs_diagonalize_symmetric() [3/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as fs_diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 1308 of file gm2_linalg.hpp.

◆ fs_diagonalize_symmetric() [4/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as fs_diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of fs_diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 1329 of file gm2_linalg.hpp.

◆ fs_diagonalize_symmetric() [5/5]

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as fs_diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_diagonalize_symmetric(m, s) for the other parameters.

Definition at line 1369 of file gm2_linalg.hpp.

◆ fs_diagonalize_symmetric_errbd()

template<class Real , class Scalar , int N>

void gm2calc::fs_diagonalize_symmetric_errbd	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 1261 of file gm2_linalg.hpp.

◆ fs_svd() [1/8]

template<class Real , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Real, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< std::complex< Real >, M, M > &	u,
		Eigen::Matrix< std::complex< Real >, N, N > &	v
	)

Singular value decomposition of M-by-N real matrix m such that.

sigma.setZero(); sigma.diagonal() = s;
m == u.transpose() * sigma * v
// convention of Haber and Kane, Phys. Rept. 117 (1985) 75-263

and (s >= 0).all(). Elements of s are in ascending order. The above decomposition can be put in the form

m == u.transpose() * s.matrix().asDiagonal() * v

if M == N.

Template Parameters

Real	type of real and imaginary parts
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N real matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M complex unitary matrix
[out]	v	N-by-N complex unitary matrix

Note: This is a convenience overload for the case where the type of u and v (complex) differs from that of m (real). Mathematically, real u and v are enough to accommodate SVD of any real m.

Definition at line 1202 of file gm2_linalg.hpp.

◆ fs_svd() [2/8]

template<class Real , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Real, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< std::complex< Real >, M, M > &	u,
		Eigen::Matrix< std::complex< Real >, N, N > &	v,
		Real &	s_errbd
	)

Same as fs_svd(m, s, u, v) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_svd(m, s, u, v) for the other parameters.

Definition at line 1223 of file gm2_linalg.hpp.

◆ fs_svd() [3/8]

template<class Real , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Real, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< std::complex< Real >, M, M > &	u,
		Eigen::Matrix< std::complex< Real >, N, N > &	v,
		Real &	s_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	u_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	v_errbd
	)

Same as fs_svd(m, s, u, v, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of fs_svd(m, s, u, v, s_errbd) for the other parameters.

Definition at line 1246 of file gm2_linalg.hpp.

◆ fs_svd() [4/8]

template<class Real , class Scalar , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s
	)

Returns singular values of M-by-N matrix m via s such that (s >= 0).all().

Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and v
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values

Definition at line 1149 of file gm2_linalg.hpp.

◆ fs_svd() [5/8]

template<class Real , class Scalar , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	v
	)

Singular value decomposition of M-by-N matrix m such that.

sigma.setZero(); sigma.diagonal() = s;
m == u.transpose() * sigma * v
// convention of Haber and Kane, Phys. Rept. 117 (1985) 75-263

and (s >= 0).all(). Elements of s are in ascending order. The above decomposition can be put in the form

m == u.transpose() * s.matrix().asDiagonal() * v

if M == N.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and v
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M unitary matrix
[out]	v	N-by-N unitary matrix

Definition at line 1081 of file gm2_linalg.hpp.

◆ fs_svd() [6/8]

template<class Real , class Scalar , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	v,
		Real &	s_errbd
	)

Same as fs_svd(m, s, u, v) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_svd(m, s, u, v) for the other parameters.

Definition at line 1102 of file gm2_linalg.hpp.

◆ fs_svd() [7/8]

template<class Real , class Scalar , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	v,
		Real &	s_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	u_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	v_errbd
	)

Same as fs_svd(m, s, u, v, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of fs_svd(m, s, u, v, s_errbd) for the other parameters.

Definition at line 1125 of file gm2_linalg.hpp.

◆ fs_svd() [8/8]

template<class Real , class Scalar , int M, int N>

void gm2calc::fs_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Real &	s_errbd
	)

Same as fs_svd(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of fs_svd(m, s) for the other parameters.

Definition at line 1167 of file gm2_linalg.hpp.

◆ fs_svd_errbd()

template<class Real , class Scalar , int M, int N>

void gm2calc::fs_svd_errbd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u = `0`,
		Eigen::Matrix< Scalar, N, N > *	v = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *	u_errbd = `0`,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *	v_errbd = `0`
	)

Definition at line 1044 of file gm2_linalg.hpp.

◆ FSZ()

double gm2calc::FSZ	(	double	x,
		double	y
	)

noexcept

Barr-Zee 2-loop function with fermion loop and scalar and Z boson mediators.

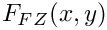
$F_{FZ}(x,y)$

Parameters

x	squared mass ratio (mf/ms)^2.
y	squared mass ratio (mf/mz)^2.

Definition at line 840 of file gm2_ffunctions.cpp.

◆ G3()

double gm2calc::G3 ( double x )

noexcept

, Eq (6.4a) arXiv:1311.1775

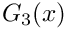
Definition at line 495 of file gm2_ffunctions.cpp.

◆ G4()

double gm2calc::G4 ( double x )

noexcept

, Eq (6.4b) arXiv:1311.1775

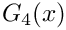
Definition at line 505 of file gm2_ffunctions.cpp.

◆ hermitian_eigen()

template<class Real , class Scalar , int N>

void gm2calc::hermitian_eigen	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	w,
		Eigen::Matrix< Scalar, N, N > *	z
	)

Definition at line 53 of file gm2_linalg.hpp.

◆ Iabc()

double gm2calc::Iabc	(	double	a,
		double	b,
		double	c
	)

noexcept

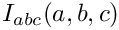
$I_{abc}(a,b,c)$ (arguments are interpreted as unsquared)

Definition at line 608 of file gm2_ffunctions.cpp.

◆ is_equal() [1/2]

template<class Derived >

bool gm2calc::is_equal	(	const Eigen::ArrayBase< Derived > &	a,
		const Eigen::ArrayBase< Derived > &	b,
		double	precision_goal
	)

Definition at line 41 of file gm2_eigen_utils.hpp.

◆ is_equal() [2/2]

template<typename T >

bool gm2calc::is_equal	(	T	a,
		T	b,
		T	eps
	)

noexcept

Definition at line 59 of file gm2_numerics.hpp.

◆ is_equal_rel()

template<typename T >

bool gm2calc::is_equal_rel	(	T	a,
		T	b,
		T	eps
	)

noexcept

Definition at line 65 of file gm2_numerics.hpp.

◆ is_zero() [1/2]

template<class Derived >

bool gm2calc::is_zero	(	const Eigen::ArrayBase< Derived > &	a,
		double	eps
	)

Definition at line 49 of file gm2_eigen_utils.hpp.

◆ is_zero() [2/2]

template<typename T >

bool gm2calc::is_zero	(	T	a,
		T	eps
	)

noexcept

Definition at line 53 of file gm2_numerics.hpp.

◆ lambda_2()

double gm2calc::lambda_2	(	double	x,
		double	y,
		double	z
	)

noexcept

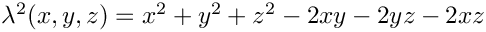
Källén lambda function $\lambda^2(x,y,z) = x^2 + y^2 + z^2 - 2xy - 2yz - 2xz$ .

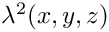
Källén lambda function $\lambda^2(x, y, z)$ .

The arguments u and v are interpreted as squared masses.

Parameters

x	squared mass
y	squared mass
z	squared mass

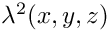
Returns: $\lambda^2(x,y,z)$

Definition at line 969 of file gm2_ffunctions.cpp.

◆ lambda_mu_cha()

Eigen::Matrix< std::complex< double >, 3, 3 > gm2calc::lambda_mu_cha ( const MSSMNoFV_onshell & model )

Calculates $\lambda_{\mu}$ , Eq (65), and $\lambda_{\chi_k^+}$ , Eq (66) arXiv:hep-ph/0609168.

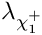
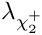
Row 0 contains $\lambda_{\chi_1^+}$ , Eq. (66). Row 1 contains $\lambda_{\chi_2^+}$ , Eq. (66). Row 2 contains $\lambda_{\mu}$ , Eq. (65).

includes tan(beta) resummation

Definition at line 447 of file gm2_2loop.cpp.

◆ lambda_sbot()

Eigen::Matrix< std::complex< double >, 2, 2 > gm2calc::lambda_sbot ( const MSSMNoFV_onshell & model )

Calculates $\lambda_{\tilde{b}_i}$ , Eq (68) arXiv:hep-ph/0609168.

includes tan(beta) resummation

Definition at line 520 of file gm2_2loop.cpp.

◆ lambda_stau()

Eigen::Matrix< std::complex< double >, 2, 2 > gm2calc::lambda_stau ( const MSSMNoFV_onshell & model )

Calculates 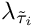$\lambda_{\tilde{\tau}_i}$ , Eq (69) arXiv:hep-ph/0609168.

includes tan(beta) resummation

Definition at line 552 of file gm2_2loop.cpp.

◆ lambda_stop()

Eigen::Matrix< std::complex< double >, 2, 2 > gm2calc::lambda_stop ( const MSSMNoFV_onshell & model )

Calculates 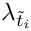$\lambda_{\tilde{t}_i}$ , Eq (67) arXiv:hep-ph/0609168.

Definition at line 486 of file gm2_2loop.cpp.

◆ log_scale()

double gm2calc::log_scale ( const MSSMNoFV_onshell & model )

Calculates 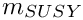$m_{SUSY}$ , p.37 arxiv:1311.1775.

Finds minimum of special masses to normalize logarithms.

Definition at line 126 of file gm2_2loop.cpp.

◆ make_raii_save()

template<typename T >

constexpr RAII_save< T > gm2calc::make_raii_save ( T & var )

constexpr

Definition at line 44 of file gm2_raii.hpp.

◆ move_goldstone_to()

template<typename DerivedArray , typename DerivedMatrix >

void gm2calc::move_goldstone_to	(	int	idx,
		double	mass,
		Eigen::ArrayBase< DerivedArray > &	v,
		Eigen::MatrixBase< DerivedMatrix > &	z
	)

The element of v, which is closest to mass, is moved to the position idx.

Parameters

idx	new index of the mass eigenvalue
mass	mass to compare against
v	vector of masses
z	corresponding mixing matrix

Definition at line 88 of file gm2_eigen_utils.hpp.

◆ n_L()

Eigen::Array< std::complex< double >, 4, 2 > gm2calc::n_L ( const MSSMNoFV_onshell & model )

Calculates 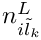$n^L_{i\tilde{l}_k}$ , Eq (2.5o) of arXiv:1311.1775, for $l=\mu$ .

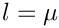
Definition at line 131 of file gm2_1loop.cpp.

◆ n_R()

Eigen::Array< std::complex< double >, 4, 2 > gm2calc::n_R ( const MSSMNoFV_onshell & model )

Calculates 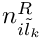$n^R_{i\tilde{l}_k}$ , Eq (2.5p) of arXiv:1311.1775, with $l=\mu$ .

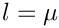
Definition at line 157 of file gm2_1loop.cpp.

◆ normalize_to_interval()

template<int M, int N>

void gm2calc::normalize_to_interval	(	Eigen::Matrix< double, M, N > &	m,
		double	min = `-1.`,
		double	max = `1.`
	)

Normalize each element of the given real matrix to be within the interval [min, max].

Values < min are set to min. Values > max are set to max.

Parameters

m	matrix
min	minimum
max	maximum

Definition at line 64 of file gm2_eigen_utils.hpp.

◆ operator<<() [1/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	os,
		const MSSMNoFV_onshell &	model
	)

streaming operator

Definition at line 891 of file MSSMNoFV_onshell.cpp.

◆ operator<<() [2/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const SM &	sm
	)

streaming operator

Definition at line 155 of file SM.cpp.

◆ operator<<() [3/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const THDM &	model
	)

streaming operator

Definition at line 648 of file THDM.cpp.

◆ operator<<() [4/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const MSSMNoFV_onshell_mass_eigenstates &	model
	)

Definition at line 1005 of file MSSMNoFV_onshell_mass_eigenstates.cpp.

◆ operator<<() [5/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const MSSMNoFV_onshell_physical &	phys_pars
	)

Definition at line 148 of file MSSMNoFV_onshell_physical.cpp.

◆ operator<<() [6/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const MSSMNoFV_onshell_problems &	problems
	)

Definition at line 177 of file MSSMNoFV_onshell_problems.cpp.

◆ operator<<() [7/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const MSSMNoFV_onshell_soft_parameters &	soft_pars
	)

Definition at line 45 of file MSSMNoFV_onshell_soft_parameters.cpp.

◆ operator<<() [8/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const MSSMNoFV_onshell_susy_parameters &	susy_pars
	)

Definition at line 39 of file MSSMNoFV_onshell_susy_parameters.cpp.

◆ operator<<() [9/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const THDM_mass_eigenstates &	model
	)

Definition at line 529 of file THDM_mass_eigenstates.cpp.

◆ operator<<() [10/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const THDM_parameters &	pars
	)

Definition at line 53 of file THDM_parameters.cpp.

◆ operator<<() [11/11]

std::ostream & gm2calc::operator<<	(	std::ostream &	ostr,
		const THDM_problems &	problems
	)

Definition at line 107 of file THDM_problems.cpp.

◆ Phi()

double gm2calc::Phi	(	double	x,
		double	y,
		double	z
	)

noexcept

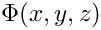
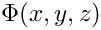
$\Phi(x,y,z)$ function from arxiv:1607.06292 Eq.

$\Phi(x,y,z)$ with squared masses, Davydychev and Tausk, Nucl. Phys. B397 (1993) 23

(68).

Note: The arguments x, y and z are interpreted as squared masses.; Proportional to Phi from Davydychev and Tausk, Nucl. Phys. B397 (1993) 23

Parameters

x	squared mass
y	squared mass
z	squared mass

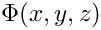
Returns: $\Phi(x,y,z)$

Definition at line 987 of file gm2_ffunctions.cpp.

◆ pow3()

template<typename T >

T gm2calc::pow3 ( T x )

noexcept

returns number to the third power

Definition at line 35 of file gm2_numerics.hpp.

◆ pow4()

template<typename T >

T gm2calc::pow4 ( T x )

noexcept

returns number to the 4th power

Definition at line 38 of file gm2_numerics.hpp.

◆ remove_if_equal()

template<class Real , int Nsrc, int Ncmp>

Eigen::Array< Real, Nsrc - Ncmp, 1 > gm2calc::remove_if_equal	(	const Eigen::Array< Real, Nsrc, 1 > &	src,
		const Eigen::Array< Real, Ncmp, 1 > &	cmp
	)

Returns all elements from src, which are not close to the elements in cmp.

The returned vector will have the length (src.size() - cmp.size()).

Parameters

src	source vector
cmp	vector with elements to compare against

Returns: vector with elements of src not close to cmp

Definition at line 118 of file gm2_eigen_utils.hpp.

◆ reorder_diagonalize_symmetric() [1/5]

template<class Real , class Scalar , int N>

void gm2calc::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s
	)

Returns singular values of N-by-N symmetric matrix m via s such that (s >= 0).all().

Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values

Definition at line 1016 of file gm2_linalg.hpp.

◆ reorder_diagonalize_symmetric() [2/5]

template<class Real , class Scalar , int N>

void gm2calc::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u
	)

Diagonalizes N-by-N symmetric matrix m so that.

m == u * s.matrix().asDiagonal() * u.transpose()

and (s >= 0).all(). Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m
N	number of rows and columns in m and u

Parameters

[in]	m	N-by-N symmetric matrix to be decomposed
[out]	s	array of length N to contain singular values
[out]	u	N-by-N complex unitary matrix

Definition at line 954 of file gm2_linalg.hpp.

◆ reorder_diagonalize_symmetric() [3/5]

template<class Real , class Scalar , int N>

void gm2calc::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd
	)

Same as reorder_diagonalize_symmetric(m, s, u) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_diagonalize_symmetric(m, s, u) for the other parameters.

Definition at line 974 of file gm2_linalg.hpp.

◆ reorder_diagonalize_symmetric() [4/5]

template<class Real , class Scalar , int N>

void gm2calc::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > &	u,
		Real &	s_errbd,
		Eigen::Array< Real, N, 1 > &	u_errbd
	)

Same as reorder_diagonalize_symmetric(m, s, u, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] u_errbd array of approximate error bounds for u

See the documentation of reorder_diagonalize_symmetric(m, s, u, s_errbd) for the other parameters.

Definition at line 995 of file gm2_linalg.hpp.

◆ reorder_diagonalize_symmetric() [5/5]

template<class Real , class Scalar , int N>

void gm2calc::reorder_diagonalize_symmetric	(	const Eigen::Matrix< Scalar, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Real &	s_errbd
	)

Same as reorder_diagonalize_symmetric(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_diagonalize_symmetric(m, s) for the other parameters.

Definition at line 1035 of file gm2_linalg.hpp.

◆ reorder_diagonalize_symmetric_errbd() [1/2]

template<class Real , int N>

void gm2calc::reorder_diagonalize_symmetric_errbd	(	const Eigen::Matrix< Real, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 915 of file gm2_linalg.hpp.

◆ reorder_diagonalize_symmetric_errbd() [2/2]

template<class Real , int N>

void gm2calc::reorder_diagonalize_symmetric_errbd	(	const Eigen::Matrix< std::complex< Real >, N, N > &	m,
		Eigen::Array< Real, N, 1 > &	s,
		Eigen::Matrix< std::complex< Real >, N, N > *	u = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real, N, 1 > *	u_errbd = `0`
	)

Definition at line 901 of file gm2_linalg.hpp.

◆ reorder_svd() [1/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s
	)

Returns singular values of M-by-N matrix m via s such that (s >= 0).all().

Elements of s are in ascending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values

Definition at line 873 of file gm2_linalg.hpp.

◆ reorder_svd() [2/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh
	)

Singular value decomposition of M-by-N matrix m such that.

sigma.setZero(); sigma.diagonal() = s;
m == u * sigma * vh    // LAPACK convention

and (s >= 0).all(). Elements of s are in ascending order. The above decomposition can be put in the form

m == u * s.matrix().asDiagonal() * vh

if M == N.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M unitary matrix
[out]	vh	N-by-N unitary matrix

Definition at line 805 of file gm2_linalg.hpp.

◆ reorder_svd() [3/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd
	)

Same as reorder_svd(m, s, u, vh) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_svd(m, s, u, vh) for the other parameters.

Definition at line 826 of file gm2_linalg.hpp.

◆ reorder_svd() [4/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	u_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	v_errbd
	)

Same as reorder_svd(m, s, u, vh, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of reorder_svd(m, s, u, vh, s_errbd) for the other parameters.

Definition at line 849 of file gm2_linalg.hpp.

◆ reorder_svd() [5/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::reorder_svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Real &	s_errbd
	)

Same as reorder_svd(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of reorder_svd(m, s) for the other parameters.

Definition at line 892 of file gm2_linalg.hpp.

◆ reorder_svd_errbd()

template<class Real , class Scalar , int M, int N>

void gm2calc::reorder_svd_errbd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u = `0`,
		Eigen::Matrix< Scalar, N, N > *	vh = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *	u_errbd = `0`,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *	v_errbd = `0`
	)

Definition at line 755 of file gm2_linalg.hpp.

◆ reorder_vector() [1/2]

template<class Derived >

void gm2calc::reorder_vector	(	Eigen::Array< double, Eigen::MatrixBase< Derived >::RowsAtCompileTime, 1 > &	v,
		const Eigen::MatrixBase< Derived > &	matrix
	)

reorders vector v according to ordering of diagonal elements in mass_matrix

Parameters

v	vector with elementes to be reordered
matrix	matrix with diagonal elements with reference ordering

Definition at line 167 of file gm2_eigen_utils.hpp.

◆ reorder_vector() [2/2]

template<class Real , int N>

void gm2calc::reorder_vector	(	Eigen::Array< Real, N, 1 > &	v,
		const Eigen::Array< Real, N, 1 > &	v2
	)

reorders vector v according to ordering in vector v2

Parameters

v	vector with elementes to be reordered
v2	vector with reference ordering

Definition at line 145 of file gm2_eigen_utils.hpp.

◆ sign()

int gm2calc::sign ( double x )

noexcept

returns sign of real number

Definition at line 27 of file gm2_numerics.cpp.

◆ signed_abs_sqrt()

double gm2calc::signed_abs_sqrt ( double x )

noexcept

returns square root of absolute of number, times sign

Definition at line 35 of file gm2_numerics.cpp.

◆ signed_sqr()

double gm2calc::signed_sqr ( double x )

noexcept

returns square of number, times sign

Definition at line 31 of file gm2_numerics.cpp.

◆ sqr()

template<typename T >

T gm2calc::sqr ( T x )

noexcept

returns number squared

Definition at line 29 of file gm2_numerics.hpp.

◆ svd() [1/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s
	)

Returns singular values of M-by-N matrix m via s such that (s >= 0).all().

Elements of s are in descending order.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values

Definition at line 317 of file gm2_linalg.hpp.

◆ svd() [2/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh
	)

Singular value decomposition of M-by-N matrix m such that.

sigma.setZero(); sigma.diagonal() = s;
m == u * sigma * vh    // LAPACK convention

and (s >= 0).all(). Elements of s are in descending order. The above decomposition can be put in the form

m == u * s.matrix().asDiagonal() * vh

if M == N.

Template Parameters

Real	type of real and imaginary parts of Scalar
Scalar	type of elements of m, u, and vh
M	number of rows in m
N	number of columns in m

Parameters

[in]	m	M-by-N matrix to be decomposed
[out]	s	array of length min(M,N) to contain singular values
[out]	u	M-by-M unitary matrix
[out]	vh	N-by-N unitary matrix

Definition at line 250 of file gm2_linalg.hpp.

◆ svd() [3/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd
	)

Same as svd(m, s, u, vh) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of svd(m, s, u, vh) for the other parameters.

Definition at line 270 of file gm2_linalg.hpp.

◆ svd() [4/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > &	u,
		Eigen::Matrix< Scalar, N, N > &	vh,
		Real &	s_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	u_errbd,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	v_errbd
	)

Same as svd(m, s, u, vh, s_errbd) except that approximate error bounds for the singular vectors are returned as well.

The error bounds are estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out]	u_errbd	array of approximate error bounds for u
[out]	v_errbd	array of approximate error bounds for vh

See the documentation of svd(m, s, u, vh, s_errbd) for the other parameters.

Definition at line 293 of file gm2_linalg.hpp.

◆ svd() [5/5]

template<class Real , class Scalar , int M, int N>

void gm2calc::svd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Real &	s_errbd
	)

Same as svd(m, s) except that an approximate error bound for the singular values is returned as well.

The error bound is estimated following the method presented at http://www.netlib.org/lapack/lug/node96.html.

Parameters

[out] s_errbd approximate error bound for the elements of s

See the documentation of svd(m, s) for the other parameters.

Definition at line 335 of file gm2_linalg.hpp.

◆ svd_eigen()

template<class Real , class Scalar , int M, int N>

void gm2calc::svd_eigen	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u,
		Eigen::Matrix< Scalar, N, N > *	vh
	)

Definition at line 39 of file gm2_linalg.hpp.

◆ svd_errbd()

template<class Real , class Scalar , int M, int N>

void gm2calc::svd_errbd	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u = `0`,
		Eigen::Matrix< Scalar, N, N > *	vh = `0`,
		Real *	s_errbd = `0`,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *	u_errbd = `0`,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > *	v_errbd = `0`
	)

Definition at line 197 of file gm2_linalg.hpp.

◆ svd_internal()

template<class Real , class Scalar , int M, int N>

void gm2calc::svd_internal	(	const Eigen::Matrix< Scalar, M, N > &	m,
		Eigen::Array< Real,(((M)<(N)) ?(M) :(N)), 1 > &	s,
		Eigen::Matrix< Scalar, M, M > *	u,
		Eigen::Matrix< Scalar, N, N > *	vh
	)

Definition at line 187 of file gm2_linalg.hpp.

◆ symmetrize()

template<typename Derived >

void gm2calc::symmetrize ( Eigen::MatrixBase< Derived > & m )

Definition at line 175 of file gm2_eigen_utils.hpp.

◆ tan_alpha()

double gm2calc::tan_alpha ( const MSSMNoFV_onshell & model )

The following functions include resummation of 1/(1 + Delta_mu) within the muon, tau and bottom Yukawa couplings.

Calculates CP-even Higgs mixing angle 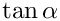$\tan\alpha$ .

Note: the result is < 0

Definition at line 426 of file gm2_2loop.cpp.

◆ tan_beta_cor()

double gm2calc::tan_beta_cor ( const MSSMNoFV_onshell & model )

Calculates $\frac{1}{1 + \Delta_{\mu}}$ .

Parameters

model model parameters

Returns: $\frac{1}{1 + \Delta_{\mu}}$

Definition at line 386 of file gm2_1loop.cpp.

◆ x_im()

Eigen::Array< double, 4, 2 > gm2calc::x_im ( const MSSMNoFV_onshell & model )

Calculates 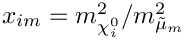$x_{im} = m^2_{\chi_i^0} / m^2_{\tilde{\mu}_m}$ , which appears in Eq (46) of arXiv:hep-ph/0609168.

squared neutralino smuon mass ratio

Definition at line 249 of file gm2_1loop.cpp.

◆ x_k()

Eigen::Array< double, 2, 1 > gm2calc::x_k ( const MSSMNoFV_onshell & model )

Calculates 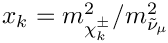$x_k = m^2_{\chi_k^\pm} / m^2_{\tilde{\nu}_\mu}$ , which appears in Eq (47) of arXiv:hep-ph/0609168.

squared chargino muon-sneutrino mass ratio

Definition at line 261 of file gm2_1loop.cpp.

Variable Documentation

◆ ALPHA_EM_MZ

constexpr double gm2calc::ALPHA_EM_MZ = ALPHA_EM_THOMPSON / (1 - DELTA_ALPHA_EM_MZ)

constexpr

Definition at line 35 of file gm2_constants.hpp.

◆ ALPHA_EM_THOMPSON

constexpr double gm2calc::ALPHA_EM_THOMPSON = 1.0/137.035999084

constexpr

Definition at line 25 of file gm2_constants.hpp.

◆ ALPHA_S_MZ

constexpr double gm2calc::ALPHA_S_MZ = 0.1184

constexpr

Definition at line 38 of file gm2_constants.hpp.

◆ CKM_DELTA

constexpr double gm2calc::CKM_DELTA = 0

constexpr

Definition at line 85 of file gm2_constants.hpp.

◆ CKM_THETA12

constexpr double gm2calc::CKM_THETA12 = 0.229206

constexpr

Definition at line 77 of file gm2_constants.hpp.

◆ CKM_THETA13

constexpr double gm2calc::CKM_THETA13 = 0.003960

constexpr

Definition at line 80 of file gm2_constants.hpp.

◆ CKM_THETA23

constexpr double gm2calc::CKM_THETA23 = 0.042223

constexpr

Definition at line 83 of file gm2_constants.hpp.

◆ DELTA_ALPHA_EM_MZ

constexpr double gm2calc::DELTA_ALPHA_EM_MZ

constexpr

Initial value:

=
      + 0.0314979  
      - 0.00007180 
      + 0.027611

Definition at line 29 of file gm2_constants.hpp.

◆ MBMB

constexpr double gm2calc::MBMB = 4.18

constexpr

Definition at line 65 of file gm2_constants.hpp.

◆ MC

constexpr double gm2calc::MC = 1.28

constexpr

Definition at line 53 of file gm2_constants.hpp.

◆ MD

constexpr double gm2calc::MD = 0.0047

constexpr

Definition at line 59 of file gm2_constants.hpp.

◆ ME

constexpr double gm2calc::ME = 0.000510998928

constexpr

Definition at line 68 of file gm2_constants.hpp.

◆ MH

constexpr double gm2calc::MH = 125.09

constexpr

Definition at line 41 of file gm2_constants.hpp.

◆ ML

constexpr double gm2calc::ML = 1.777

constexpr

Definition at line 74 of file gm2_constants.hpp.

◆ MM

constexpr double gm2calc::MM = 0.1056583715

constexpr

Definition at line 71 of file gm2_constants.hpp.

◆ MS

constexpr double gm2calc::MS = 0.096

constexpr

Definition at line 62 of file gm2_constants.hpp.

◆ MT

constexpr double gm2calc::MT = 173.34

constexpr

Definition at line 56 of file gm2_constants.hpp.

◆ MU

constexpr double gm2calc::MU = 0.0022

constexpr

Definition at line 50 of file gm2_constants.hpp.

◆ MW

constexpr double gm2calc::MW = 80.385

constexpr

Definition at line 44 of file gm2_constants.hpp.

◆ MZ

constexpr double gm2calc::MZ = 91.1876

constexpr

Definition at line 47 of file gm2_constants.hpp.

Namespaces

Classes

Functions

Variables

Function Documentation

◆ AAC()

◆ AAN()

◆ abs_sqrt()

◆ amu1Lapprox()

◆ amu1Lapprox_non_tan_beta_resummed()

◆ amu1LBHmuL()

◆ amu1LBHmuR()

◆ amu1LBmuLmuR()

◆ amu1LChi0()

◆ amu1LChipm()

◆ amu1LWHmuL()

◆ amu1LWHnu()

◆ amu2LaCha()

◆ amu2LaSferm()

◆ amu2LBHmuL()

◆ amu2LBHmuR()

◆ amu2LBmuLmuR()

◆ amu2LChi0Photonic()

◆ amu2LChipmPhotonic()

◆ amu2LFSfapprox()

◆ amu2LFSfapprox_non_tan_beta_resummed()

◆ amu2LWHmuL()

◆ amu2LWHnu()

◆ BBC()

◆ BBN()

◆ c_L()

◆ c_R()

◆ calculate_amu_1loop() [1/2]

◆ calculate_amu_1loop() [2/2]

◆ calculate_amu_1loop_non_tan_beta_resummed()

◆ calculate_amu_2loop() [1/2]

◆ calculate_amu_2loop() [2/2]

◆ calculate_amu_2loop_bosonic()

◆ calculate_amu_2loop_fermionic()

◆ calculate_amu_2loop_non_tan_beta_resummed()

◆ calculate_mb_SM5_DRbar()

◆ calculate_mb_SM6_MSbar()

◆ calculate_mt_SM6_MSbar()

◆ calculate_mtau_SM6_MSbar()

◆ calculate_uncertainty_amu_0loop() [1/4]

◆ calculate_uncertainty_amu_0loop() [2/4]

◆ calculate_uncertainty_amu_0loop() [3/4]

◆ calculate_uncertainty_amu_0loop() [4/4]

◆ calculate_uncertainty_amu_1loop() [1/4]

◆ calculate_uncertainty_amu_1loop() [2/4]

◆ calculate_uncertainty_amu_1loop() [3/4]

◆ calculate_uncertainty_amu_1loop() [4/4]

◆ calculate_uncertainty_amu_2loop() [1/3]

◆ calculate_uncertainty_amu_2loop() [2/3]

◆ calculate_uncertainty_amu_2loop() [3/3]

◆ clausen_2()

◆ closest_index()

◆ cube()

◆ delta_bottom_correction()

◆ delta_down_lepton_correction()

◆ delta_g1()

◆ delta_g2()

◆ delta_mu_correction()

◆ delta_tan_beta()

◆ delta_tau_correction()

◆ delta_yuk_bino_higgsino()

◆ delta_yuk_higgsino()

◆ delta_yuk_wino_higgsino()

◆ diagonalize_hermitian() [1/5]

◆ diagonalize_hermitian() [2/5]

◆ diagonalize_hermitian() [3/5]

◆ diagonalize_hermitian() [4/5]

◆ diagonalize_hermitian() [5/5]

◆ diagonalize_hermitian_errbd()

◆ diagonalize_hermitian_internal()

◆ diagonalize_symmetric() [1/10]

◆ diagonalize_symmetric() [2/10]

◆ diagonalize_symmetric() [3/10]

◆ diagonalize_symmetric() [4/10]

◆ diagonalize_symmetric() [5/10]